Популярная физика. От архимедова рычага до квантовой теории - читать онлайн книгу. Автор: Айзек Азимов cтр.№ 58

Давайте рассмотрим еще две ноты с частотами 250/с и 252/с соответственно. Тогда после половины секунды одна нота закончит 125 колебаний, а другая — 126 колебаний, и они возвратятся в фазу, соответствующую гребню. Это будет повторяться каждую половину секунды, то есть будут получаться два биения в секунду. Число биений в секунду, в случае одновременного звучания двух нот, равно разности в частоте этих двух нот.

Если биения настольно редкие, что их можно различимо услышать, то они создают звуковые комбинации, неприятные для слуха. Наиболее неприятным является, очевидно, 30 биений в секунду. Однако в том случае, когда число биений в секунду больше 60, они взаимопроникают друг в друга, и для человеческого уха их комбинация кажется приятной или гармоничной.

Теперь давайте рассмотрим две ноты, у которых одна имеет частоту точно в два раза больше другой. Например, первая имеет частоту 220/с, а вторая — 440/с; отношение частот равно 1:2. Число биений, когда ноты звучат вместе, равно 440—220, или 220 раз в секунду. Биения дублируют ноту более низкого тона, так что кажется, что две ноты «сплавляются» друг с другом и начинают представлять собой одну и ту же ноту. Они гармонируют друг с другом.

Именно Пифагор был первым, кто заметил, что гармонирующие ноты связаны между собой целочисленными отношениями небольшой величины. У него не было никакой аппаратуры для непосредственного измерения самой частоты, но он рассмотрел струны различной длины. Он обнаружил, что две струны с длинами, относящимися как 1:2, производят приятную комбинацию, так же как струны с соотношением длин 2:3 и 3:4.

(Результаты этих наблюдений за звуком были истолкованы Пифагором с мистической точки зрения. Он рассматривал роль взаимодействия небольших целочисленных отношений в создании благозвучий в соответствии со своими взглядами о том, что вся Вселенная управляется числами. Он и его ученики предполагали, что и сами планеты способны создавать звуки — так называемую «музыку сфер», ноты в которой основаны на их расстояниях относительно Земли. Наука не могла освободиться от этих заблуждений в течение 2000 лет.)

Предположим тогда, что мы начинаем с ноты, частота которой равна 440/с (стандартная частота для музыкантов); назовем эту ноту А. Нота вдвое большей частоты звучит настолько подобно этой, что мы можем предположить, что это — тоже А, то есть мы можем использовать эту букву для обозначения ноты с частотой, равной половине А. Таким образом, фактически мы получим целый ряд значений такого А, с частотами, равными 110/с, 220/с, 440/с, 880/с, 1760/с и так далее, расширяя диапазон, из которого мы выбираем, на неопределенное значение вверх и вниз.

Между любыми двумя последовательными нотами А мы можем поставить другие ноты с частотами, которые состоят в некоторых других последовательных арифметических отношениях к нотам А и друг к другу. Общепринято подставлять в этот интервал шесть других нот; они обозначаются буквами В, С, D, Е, F и G. Таким образом, в интервале от А до А мы имеем ноты: А, В, С, D, E, F, G, А. В интервале от А до А располагаются восемь нот (считая и А), между которыми находятся семь интервалов. Поэтому интервал от А до А называется октавой (от латинского слова, означающего «восьмой».) Другие интервалы называются по-английски. Интервал от С до G (С, D, E, F, G), который включает в себя пять нот, называется «пятым», в то время как интервал от С до F — «четвертым». В нашей стране, да и во всем остальном мире, кроме США, общепринята латинская система обозначения музыкальных интервалов. Согласно ей сама нота С (представляющая собой интервал от себя до себя) называется «прима», интервал от С до D называется «секунда», от С до Е — «терция», от С до F — «кварта», от С до G — «квинта», от С до А — «секста», от С до В — «септима» и, наконец, от С до С — «октава». (Все названия музыкальных интервалов происходят от латинских слов, означающих соответственно: «первый», «второй», «третий», «четвертый», «пятый», «шестой», «седьмой» и «восьмой». — Пер.)

Частоты, соответствующие нотам, в диапазоне от А (220/с) до А (880/с):

А = 220	А = 440	А = 880
В = 247,5	В = 495
С = 264	С = 528
D = 297	D = 594
Е = 330	Е = 660
F = 352	F = 704
G = 396	G = 792

Диапазон от 220/с до 440/с составляет одну октаву, а диапазон от 440/с до 880/с — другую октаву. Каждая нота в верхней октаве представляет собой удвоенную по частоте соответствующую ноту в более низкой октаве, так что интервал от В до В представляет собой октаву, так же как интервал от С до С, от D до D и так далее. Если вы запомните, что удвоение частоты создает ноты для каждой следующей более высокой октавы, а деление пополам — ноты для каждой более низкой октавы, вы сможете написать частоты для любой ноты в любой октаве.

Если мы послушаем ноты, идущие последовательно в пределах любой октавы, то обнаружим, что они звучат точно так же, как соответствующие ноты в пределах любой другой октавы: выше или ниже. Стандартная клавиатура фортепьяно охватывает диапазон немногим более семи октав; если мы будем нажимать одну за другой белые клавиши, то легко обнаружим, что одна и та же «мелодия» последовательно будет повторяться семь раз, только переходя на все более высокие тоны звуков.

Все частоты связаны между собой отношениями, которые могут быть выражены в небольших целых числах. Отношение G к С, например, равно 396:264, или 3:2; а отношение F к С равно 352:264, или 4:3. Именно эти простые отношения изучал Пифагор, и именно простота отношений обосновывает величину биений, при которых ноты «укрепляются» и хорошо «смешиваются» между собой. Именно поэтому квинты (3:2) и кварты (4:3) очень часто используются для построения благозвучных интервалов между последовательными нотами.

Таблица распределения интервалов по октаве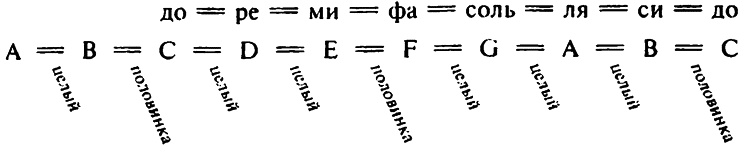

Но тогда также и отношения между тремя нотами (сочетание которых называется «основным трезвучием» или «аккордом»), С, Е и G, равное 264:330:396, или 4:5:6, будет благозвучным. F, А и С также составляют мажорное трезвучие, так же как и G, В и D. Фактически интервалы между нотами задуманы таким образом, что каждая нота может быть частью одного из этих трех мажорных трезвучий ^[55].