Популярная физика. От архимедова рычага до квантовой теории - читать онлайн книгу. Автор: Айзек Азимов cтр.№ 37

1/mv²/2 = ka²/2. (Уравнение 8.2)

Мы легко можем преобразовать это уравнение:

a/v = √(m/k). (Уравнение 8.3)

Заменив (m/k) на (a/v) в уравнении 8.1, мы получаем:

t = 2π∙√(m/k). (Уравнение 8.4)

Это совершенно удивительный результат, поскольку выясняется, что период простых гармонических колебаний зависит только от массы перемещающегося тела и пропорционален константе между нагрузкой и напряжением. Все эти данные могут легко быть определены для данного специфического тела, и, таким образом, мы можем сразу рассчитать период колебаний.

Следует отметить, что период колебаний не зависит ни от скорости тела, перемещающегося с простыми гармоническими колебаниями, ни от расстояния, на которое тело перемещено из среднего положения, так как и v и а исчезли из уравнения 8.4. Это означает, что, если струна оттянута на некоторое расстояние от ее среднего положения, она достигнет некоторой максимальной скорости в средней точке ее колебаний и будет иметь некоторый период вибрации. Если ее оттянуть на большее или меньшее расстояние, она получит большую или соответственно меньшую максимальную скорость; в любом случае изменения в скорости будет только достаточно, чтобы восполнить изменение в расстоянии смещения, так что период колебаний останется тем же самым.

Этот постоянный период вибрации является большим благом для всего человечества, потому что предлагает средство для весьма точного измерения времени — подсчет колебаний, причем даже затухающих колебаний.

Теоретически любые периодические колебания делают это возможным. Первым периодическим движением, которое служит человечеству в качестве часов, было непосредственно само движение Земли; каждый поворот планеты на ее оси отмечает один день и ночь, а каждый поворот планеты относительно Солнца отмечает один цикл сезонов. К сожалению, движения Земли не могут нам предложить хороших средств измерения промежутков времени меньше чем длиною в день.

В древние времена человечество использовало апериодические движения, разбитые (как надеялись) на равные части. Они включают в себя движение тени по основанию, движение песка через узкое отверстие, капанье воды через отверстие, сокращение длины горящей свечи и так далее. Все, что можно было получить таким способом, — это довольно приблизительно равные промежутки времени; и только в середине XVII столетия появилась возможность сообщить время с точностью до часа или менее или измерить единицы времени меньшие чем час с некоторой разумной точностью.

Только когда стали использоваться периодические колебания с короткими периодами вибрации, стали возможными современные устройства для измерения времени, а вместе с ними (до очень большой степени) и вся современная наука.

Сам Галилео весьма страдал от неспособности точно измерить короткие интервалы времени. (В некоторых случаях он использовал для замера времени свой пульс, и хотя это было периодическое явление, но, к сожалению, не очень устойчивое.) Однако хотя он непосредственно сам и не извлек выгоды из этого, он был первым, кто обнаружил периодические колебания, которые в конечном счете стали использоваться для измерения времени.

В 1583 году, когда Галилео был юношей и студентом-медиком в Университете Пизы, он однажды пошел в местный собор, чтобы помолиться. Но даже его глубокая вера (а Галилео всегда был очень набожным человеком) не смогла удержать его пытливый ум от наблюдений. Он не мог не заметить колебание паникадила ^[30] в нефе. Время от времени благодаря капризу ветра оно описывало большую дугу, время от времени — меньшую, но, как показалось Галилео, период колебаний все время был тем же самым независимо от длины дуги. Он прервал свои молитвы и проверил эту догадку, рассчитав колебания при помощи своего пульса.

Вернувшись домой, Галилео продолжил эксперимент, подвесив маленькие «люстры», сделанные из «отвесов» и нитей, к потолку и позволив им раскачиваться с различным периодом колебаний. (Такие подвешенные грузы называются «маятниками» (pendulum — от латинского слова, означающего «висение» или «покачивание».) Галилео смог доказать, что период колебания не зависел от тяжести отвесов, а только от квадратного корня из длины нити. Другими словами, маятник, подвешенный на нити длиной четыре фута, имеет период колебания вдвое больший, чем такой же, но с нитью длиной в один фут.

Теперь рассмотрим маятник. Если отвес висит вертикально на своей нити, он останется неподвижным. Это — его положение равновесия. Если отвес отклонить в сторону, натяжение нити заставит его двигаться по дуге круга так, что он поднимется на более высокий уровень. Если отпустить его, то под воздействием силы тяжести он будет двигаться вниз с увеличивающейся скоростью, назад по дуге круга, к своему самому нижнему положению.

Результирующая сила, которая вызывает это движение, получается в итоге сложения силы тяжести и силы натяжения нити. По мере снижения отвеса нить становится все более и более вертикальной и компенсирует все большую часть силы тяжести. Результирующая сила постоянно уменьшается по мере снижения отвеса, так же как ускорение. Когда отвес попадает в самую нижнюю часть дуги, маятник оказывается подвешенным на совершенно вертикальной линии, и нить полностью компенсирует все гравитационное напряжение. В этой точке не существует никакого неуравновешенного гравитационного напряжения и никакого ускорения. Отвес перемещается с максимальной скоростью.

Из-за инерции отвес проходит через точку равновесия и начинает описывать дугу в другом направлении. Теперь снова имеется результирующая сила, которая замедляет его движение. Чем выше он поднимается, тем больше неуравновешенная сила тяготения и тем быстрее замедляется движение отвеса. В конечном счете его движение замедляется до нуля, и в этот момент отвес достигает точки максимального смещения. Далее начинается обратное движение вниз, через точку равновесия, до максимального смещения с другой стороны и так далее.

Это очень похоже на описание простых гармонических колебаний, за исключением того, что там щипание струны вызывает движение вперед и назад по прямой линии, а смещение маятника вызывает движение вперед и назад по дуге круга. Как нам может показаться — это не является принципиальной и существенной разницей, потому что нам кажется, почему бы не существовать периодическому вращательному движению точно так, как существует периодическое поступательное движение? И действительно — имеется достаточное количество обоих видов этих простых гармонических колебаний.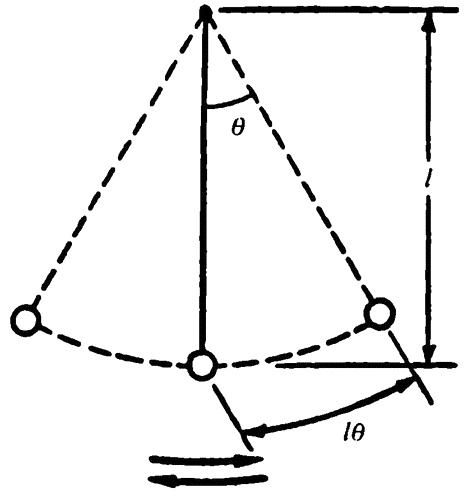

^{Маятник}

Но действительно ли движение маятника является одним из них? Во всех случаях простых гармонических колебаний типа вибрации струны, скручивающегося и раскручивающегося шнура, движения вверх и вниз натянутой струны и раскручивания и закручивания упругой спирали сила упругости находится в пределах материала, из которого изготовлен предмет, она — производное его эластичности (упругости). В случае маятника сила упругости находится вне системы в форме неуравновешенного гравитационного напряжения. Это может представлять собой принципиальную разницу. Чтобы проверить, качается ли маятник согласно свойствам простых гармонических колебаний, мы должны проверить, действительно ли является сила упругости, компенсирующая силу тяжести, прямо пропорциональной величине смещения, что служит показателем того, что в данном случае действует закон Гука (характеризующий простые гармонические колебания).