Популярная физика. От архимедова рычага до квантовой теории - читать онлайн книгу. Автор: Айзек Азимов cтр.№ 36

Всякий раз, когда движение складывается из ряда повторных поддвижений, каждое из которых имеет свой собственный период колебаний, говорят, что такое движение называется «периодическими колебаниями», особенно когда индивидуальные периоды колебаний равны. Движение по кругу или любой замкнутой кривой может рассматриваться как составленное из последовательных возвращений к первоначальной точке начала движения, с каждым отдельным движением по кривой; следовательно, это ряд повторных поддвижений и он может быть назван периодическими колебаниями. Вибрация также представляет собой ряд возвращений к первоначальной точке, хотя скорее посредством движений «вперед-назад», чем в соответствии с движением по замкнутой кривой, поэтому и вибрация может также служить примером периодических колебаний.

Определить период колебаний объекта, даже когда он вибрирует в соответствии с законами, управляющими простыми гармоническими колебаниями, довольно сложно, если иметь дело непосредственно с вибрацией. В такой вибрации величины скорости, ускорения не являются постоянными, обе они изменяются в зависимости от положения в каждый данный момент времени. Поэтому при таких исследованиях ищут пути представить вибрацию посредством некоторого вида движения, включающего в себя постоянное ускорение.

Это может быть достигнуто путем перехода от вибрации к другой форме периодических колебаний — круговому движению. Объект может быть изображен как перемещающийся по кругу при постоянном внутреннем ускорении и, следовательно, как перемещение по окружности круга с постоянной скоростью.

Если рассматриваемый круг имеет радиус длины a, тогда длина его окружности равна 2πa. Если точка перемещается со скоростью v, то время t, которое требуется, чтобы сделать полное обращение (период кругового движения), равно:

t = 2πa/v . (Уравнение 8.1)

Теперь если мы представим себе круг, бросающий тень на стену, то тень его боковой поверхности будет прямой линией. Точка, перемещающаяся по кругу, на тени будет казаться перемещающейся вперед и назад по прямой линии. По мере движения точки по окружности точка на тени будет совершать возвратно-поступательное движение по прямой линии. Период колебаний по окружности (уравнение 8.1) будет также равен периоду вибрации тени.

На любом из крайних положений линии-тени точка будет казаться перемещающейся очень медленно, потому что ее движение по кругу отражается на линию-тень под более или менее прямым углом, что дает очень немного поперечного движения. (А только поперечное движение обнаружит себя на тени.) По мере передвижения точки в промежуточные части круга его движение становится все более поперечным и все менее поступательным по отношению к линии, так что точка на тени кажется двигающейся все быстрее и быстрее, чем дальше она находится от крайнего положения. Таким образом, когда точка находится в самом центре, точка на окружности перемещается параллельно линии и все ее движение — поперечно. В центре теневой линии поэтому точка кажется перемещающейся самым быстрым образом. Движение точки по линии-тени напоминает движения тела при простых гармонических колебаниях, и действительно, данное движение является таковым. Следовательно, формула 8.1 представляет собой период (t) простых гармонических колебаний.

Уравнение 8.1 все еще представляет трудность для анализа, так как включает в себя скорость v, и, в то время как точка перемещается по окружности с постоянной скоростью, она перемещается по линии-тени с постоянно меняющейся скоростью. Поэтому мы должны найти, если возможно, что-то, что займет место v.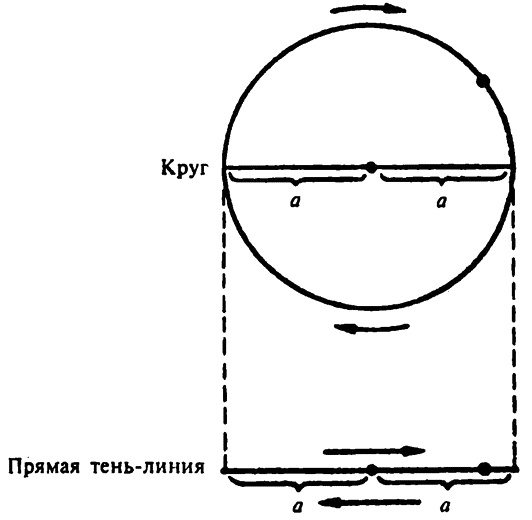

^{Периодические колебания}

В любых простых гармонических колебаниях максимальная скорость проходит через среднюю точку между двумя экстремумами. В этот момент тело, испытывающее такое движение, находится в положении равновесия, где оно и осталось бы, если бы находилось в состоянии покоя. В этой точке тело не обладает никакой потенциальной энергией, а обладает только энергией движения, или, как ее иначе называют, «кинетической энергией». Поскольку тело перемещается дальше от своего положения равновесия, оно теряет скорость и поэтому теряет кинетическую энергию. Однако оно перемещается в положение, в котором кинетическая энергия равна нулю, зато получает энергию положения, или, как ее иначе называют, «потенциальную энергию». В экстремальном положении тело останавливается на мгновение, и вся его энергия находится в форме потенциальной энергии. Тело, участвующее в простых гармонических колебаниях, демонстрирует периодический переход кинетической энергии в потенциальную энергию и обратно и (не принимая во внимание эффект демпфирования трением и сопротивление воздуха) являет собой превосходный пример сохранения механической энергии.

Как я уже сказал ранее, в соответствии с законом Гука, сила упругости, приложенная к телу, испытывающему простые гармонические колебания, пропорциональна его смещению от положения равновесия. Она равна F = kd, где F — сила упругости, а d — смещение. Сила упругости — наименьшая в положении равновесия (которое находится в центре нашей прямолинейной тени). В этой точке не имеется никакого смещения и сила упругости равна нулю. Максимальное значение силы упругости достигается в точке максимального смещения, которая, конечно, расположена на краю прямолинейной тени. Это крайнее положение равно расстоянию a (радиусу окружности, которая отбрасывает прямолинейную тень) от центра или положения равновесия, следовательно, мы можем сказать, что сила упругости в ее максимальном значении равна ka.

В то время как тело перемещается из положения равновесия до крайнего положения, оно перемещается против силы, которая начинается в 0 и плавно увеличивается до ka, а средняя сила, против которой действует перемещающееся тело, поэтому равна ka плюс 0, разделенные на два, или (ka/2).

Работа, приложенная к телу, которая необходима, чтобы вывести его из положения равновесия и переместить в данную точку, равна силе, умноженной на расстояние, на котором приложена сила. Это означает ka/2 умножить на a, или ka²/2. В крайней точке вся эта работа будет запасена в виде потенциальной энергии и поэтому максимальная потенциальная энергия тела, перемещающегося на условиях простых гармонических колебаний, равна ka²/2.

В то же самое время кинетическая энергия тела достигает своего максимального значения в средней точке, там, где вся потенциальная энергия была преобразована в движение и где скорость достигает своего максимума. Кинетическая энергия тогда равна mv²/2, где m — масса тела, a v его максимальная скорость.

Так как потенциальная энергия и кинетическая энергия постоянно конвертируются между собой в течение всего времени существования простых гармонических колебаний без существенных потерь, максимальная величина потенциальной энергии и максимальная величина кинетической энергии должны быть равны. Таким образом: