На плечах гигантов - читать онлайн книгу. Автор: Стивен Хокинг cтр.№ 52

Парадокс кротовых нор наталкивает на мысль, что если мы вернемся в прошлое, то сумеем изменить его, а следовательно, изменится и будущее. Что будет, если вернуться в прошлое и убить собственного деда до того, как он успеет зачать твоего отца или мать?

Дифференциальное уравнение Пуассона имеет вид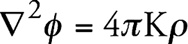

(1)

В совокупности с уравнением движения материальной точки это уравнение не может полностью заменить теорию дальнодействия Ньютона. К ним необходимо добавить условие того, что потенциал φ в пространственной бесконечности стремится к определенному пределу. Схожим образом обстоит дело и в теории тяготения, которая следует из общего принципа относительности. Здесь также к дифференциальным уравнениям должны быть добавлены граничные условия на пространственной бесконечности, если мы на самом деле рассматриваем мир бесконечно протяженным в пространстве.

В задачах, связанных с планетной системой, выбираются эти граничные условия при допущении, что можно выбрать такую координатную систему, в которой все потенциалы тяготения g_μν на пространственной бесконечности становятся постоянными. Но изначально совершенно не очевидно, что при рассмотрении более значительных областей Вселенной можно вводить те же самые граничные условия. Ниже изложим соображения, которые мы получили до настоящего времени по этому принципиально важному вопросу.

§ 1. Теория Ньютона

Граничное условие Ньютона в форме существования постоянного предела для φ в пространственной бесконечности ведет к тому, что плотность материи на бесконечности обращается в нуль. Действительно, пусть во Вселенной существует область, вокруг которой гравитационное поле материи, рассматриваемое в целом, обладает сферической симметрией (центр). Тогда из уравнения Пуассона следует, что средняя плотность ρ с увеличением расстояния r от центра должна стремиться к нулю быстрее, чем 1/r², для того чтобы φ на бесконечности стремилось к некоторому пределу ^[17]. В этом смысле мир по Ньютону конечен, хотя может обладать бесконечно большой общей массой.

Из приведенного рассуждения прежде всего следует, что излучение, испускаемое небесными телами, частично покинет мир Ньютона по радиальному от центра направлению с тем, чтобы бесследно затеряться на бесконечности. Не может ли произойти то же с целым небесным телом? Едва ли можно отрицать этот факт, поскольку из предположения о существовании конечного предела для φ в пространственной бесконечности следует, что обладающее конечной кинетической энергией небесное тело может достичь пространственной бесконечности, преодолев ньютоновские силы притяжения. Согласно статистической механике, такие события должны происходить до тех пор, пока общая энергия звездной системы достаточно велика, чтобы – при переносе ее на одно небесное тело – последнее могло совершить путешествие на бесконечность, откуда оно никогда не сможет вернуться.

Можно было бы попытаться обойти эту своеобразную трудность, допустив, что указанный граничный потенциал имеет на бесконечности очень большое значение. Это было бы приемлемо, если бы изменение потенциала тяготения не определялось самим небесным телом. В действительности мы с неизбежностью приходим к заключению, что наличие значительных разностей потенциалов гравитационного поля противоречит фактам. Наоборот, разности потенциалов должны быть такого малого порядка, чтобы определяемые ими скорости звезд не превосходили фактически наблюдаемых скоростей.

Закон Больцмана распределения молекул газа, примененный к звездам, рассматривающий звездную систему как газ, который находится в стационарном тепловом движении, приводит к тому, что ньютоновская Вселенная вообще не могла бы существовать. Это следует из того, что конечной разности потенциалов между центром и бесконечностью соответствует конечное отношение плотностей. Таким образом, нулевая плотность на бесконечности влечет за собой нулевую плотность в центре.

Эти трудности, по-видимому, нельзя преодолеть, оставаясь в рамках теории Ньютона. Возникает вопрос, нельзя ли преодолеть их путем модификации теории Ньютона. Для этого прежде всего укажем путь, который не следует принимать слишком серьезно, так как он служит только для того, чтобы лучше уяснить последующие рассуждения. Вместо уравнения Пуассона напишем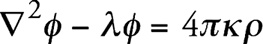

(2)

где λ представляет собой некоторую универсальную постоянную.

Если ρ₀ есть постоянная плотность распределения массы, то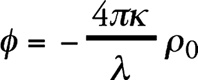

(3)

есть решение уравнения (2). Оно соответствует случаю равномерного пространственного распределения неподвижных звезд, причем плотность ρ₀ может равняться действительной средней плотности материи в мировом пространстве. Это решение соответствует бесконечно протяженному пространству, в среднем равномерно заполненному материей.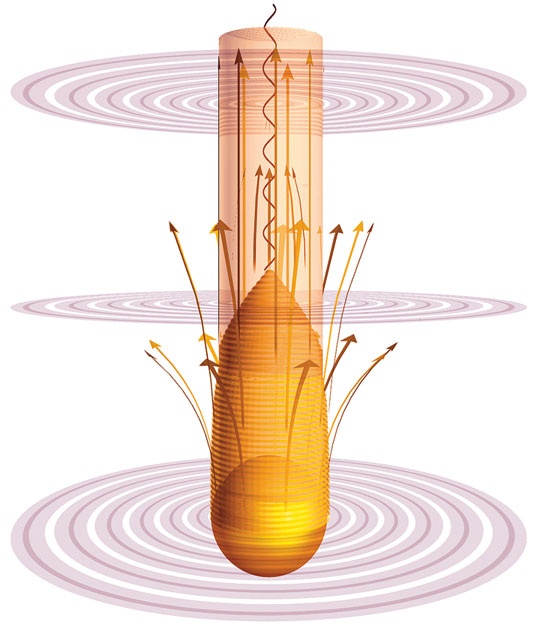

Звезда на стабильной стадии существования. Показано, что с ее поверхности исходит свет.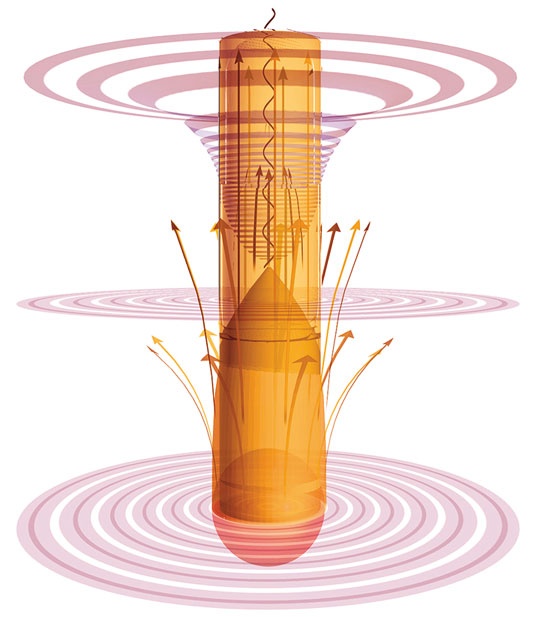

Звезда начинает схлопываться (средняя стадия), ее свет стягивается обратно к поверхности, пока не возникает граница (горизонт событий), за которую свет уже не может вырваться.

Если теперь предположить, что имеются местные неравномерности в распределении материи, не изменяющие среднего значения плотности распределения, то к постоянному значению (3) потенциала φ придется добавить дополнительную величину φ, которая вблизи более плотных масс будет тем более похожа на поле Ньютона, чем меньше αφ по сравнению с 4πΚρ.

Такой мир не имел бы центра по отношению к гравитационному полю, и не было бы надобности допускать, что плотность уменьшается на бесконечности. Наоборот, и средний потенциал, и средняя плотность были бы постоянны вплоть до бесконечности. При этом конфликт, отмеченный между теорией Ньютона и статистической механикой, отсутствовал бы. При постоянной (крайне малой) плотности материя находится в равновесии, не требуя внутренних сил (давления) для поддержания этого равновесия.