
|
||
|
|
||
|
|
Онлайн книга - Магия математики. Как найти x и зачем это нужно | Автор книги - Артур Бенджамин
Cтраница 42

Примерно то же справедливо и отношении простых чисел и умножения: любое положительное целое число можно представить в виде произведения простых чисел (с той лишь разницей, что простые числа изучены куда меньше, чем степени основания 2, и знаем о них мы далеко еще не всё). Простым числом называется целая положительная величина, имеющая только два делителя: 1 и само себя. Вот некоторые из них: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53… Число 1 простым не является: у него всего один делитель (хотя, конечно, не только поэтому – есть и более веские причины, о которых мы поговорим чуть позже). Обратите также внимание: в этом ряду всего лишь одно четное – 2, что явно (а можно сказать и – выгодно) отличает ее от остальных простых чисел. Положительное целое число, для которого имеются 3 и более делителя, называется составным, ведь его можно разложить на более простые. Вот они: 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30… Так, у четверки всего три делителя (1, 2 и 4), у шестерки – четыре (1, 2, 3 и 6) и так далее. Обратите внимание, что числа 1 нет и здесь. Математики называют его единицей, числом с уникальным свойством – быть делителем абсолютно любого целого числа. Каждое составное число может быть представлено в виде произведения простых чисел. Возьмем для примера 120. Можно начать с 120 = 6 × 20. Но и 6, и 20 – тоже составные. Разложим их сразу на простые: 6 = 2 × 3, 20 = 2 × 2 × 5. Следовательно, 120 = 2 × 2 × 2 × 3 × 5 = 2³3¹5¹ Примечательно то, что, на какие бы составляющие мы ни разложили начальное число, результат получится абсолютно тот же. Причина тому – теорема о единственности разложения, основная теорема арифметики, согласно которой каждое положительное целое число больше 1 раскладывается на произведение простых чисел единственным способом, включая порядок следования сомножителей. Здесь-то, кстати, и кроется настоящая причина того, что число 1 не может быть названо простым: будучи простым, оно бы делало эту теорему несостоятельной. Ведь тогда 12, например, можно было бы представить не только как 2 × 2 × 3, но и как 1 × 1 × 2 × 2 × 3, и разложение на простые числа не было бы уникальным. Однажды разложив число, вы узнаете всю его подноготную. В детстве моим любимым числом была девятка, но с возрастом я узнавал и другие, куда более сложные (вроде π = 3,14159…, φ = 1,618…, e = 2,71828… или число i, которое не может быть представлено в виде десятичной дроби, о чем мы подробно поговорим в главе 10) и влюблялся в них без памяти. Какое-то время моим фаворитом было 2520 – наименьшее из чисел, которые делятся на все числа от 1 до 10. Вот как оно выглядит при разложении на простые множители: 2520 = 2³3²5¹7¹ Зная положительные множители, вы можете узнать и положительные делители – вернее, их количество. Так, любой из делителей 2520 должен сводиться к форме 2a3b5c7d, где a может быть равно 0, 1, 2 или 3 (четыре варианта), b – 0, 1 или 2 (три варианта), а с – 0 или 1 (два варианта). Следовательно, согласно правилу произведения, 2520 имеет 4 × 3 × 2 × 2 = 48 положительных делителей. Отступление Из основной теоремы арифметики вытекает любопытное следствие, касающееся простых чисел (вы можете найти его доказательство практически в любом учебнике, причем на первых страницах): если простое число p является делителем произведения двух или более чисел, оно также должно являться делителем одного из них. Например, поскольку 999 999 = 333 × 3003 кратно 11, то 11 должно быть делителем либо 333, либо 3003 (на деле – только последнего сомножителя: 3003 = 11 × 273). В случае составных чисел это правило работает не всегда: так, 60 = 6 × 10 делится на 4, несмотря на то что 4 не является делителем ни 6, ни 10. Чтобы показать уникальность каждого разложения на множители, пойдем от обратного – предположим, что одно и то же число можно представить несколькими отличными друг от друга произведениями. Допустим, N – наименьшее из чисел, которые можно разложить на простые сомножители двумя разными способами. Скажем, p1p2… pr = N = q1q2… qs где все значения pi и qj суть простые величины. Так как p1 очевидно кратно N, оно должно быть делителем одного из значений qj. Облегчим себе задачу и предположим, что это q1. Тогда, поскольку q1 – величина простая, у нас должно получиться q1 = p1. Разделив все части уравнения на p1, приходим к 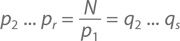
что означает, что число
Отступление Кстати, существуют такие системы счисления, где далеко не каждое число раскладывается на множители единственным способом. На Марсе, например, у каждого по две головы, поэтому марсиане понятия не имеют, что такое нечетные числа, пользуясь исключительно четными: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30… В марсианской системе числа вроде 6 или 10 будут считаться простыми, потому что их нельзя разложить на меньшие четные числа. А отличить простые числа от составных (которые, кстати, чередуются в ряду с завидной регулярностью) не составляет никакого труда: если число делится на 4 без остатка – оно составное (потому что 4k = 2 × 2k), если не делится – простое (6, 10, 14, 18 и т. д.), ведь его нельзя представить в виде двух меньших четных чисел. 
Но давайте посмотрим на число 180: 6 × 30 = 180 = 10 × 18 Очевидно, что оно может быть разложено на множители двумя разными способами, а значит, ни о какой уникальности на Марсе и слыхом не слыхивали.
|
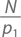 может быть разложено на множители двумя разными способами, а это противоречит нашему условию, что N есть наименьшее из таких чисел.◻
может быть разложено на множители двумя разными способами, а это противоречит нашему условию, что N есть наименьшее из таких чисел.◻ Вернуться к просмотру книги
Вернуться к просмотру книги
 Перейти к Оглавлению
Перейти к Оглавлению
 Перейти к Примечанию
Перейти к Примечанию
 © 2020 LoveRead.ec - электронная библиотека в которой можно
© 2020 LoveRead.ec - электронная библиотека в которой можно