Магия математики. Как найти x и зачем это нужно - читать онлайн книгу. Автор: Артур Бенджамин cтр.№ 39

Затем сделаем так:

и так:

При вычитании 10x из 100x все, что стоит после запятой, отсекается, оставляя нас с

Значит,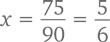

Этот алгоритм позволяет нам с определенной долей уверенности утверждать, что число будет рациональным тогда и только тогда, когда его представление в виде десятичной дроби является либо конечным, либо периодическим. Иррациональной же будет та дробь, которая после запятой имеет бесконечное количество знаков, не образуюющих при этом цикл, например,

Вернемся к теоремам о положительных числах. В главе 1 мы выяснили, что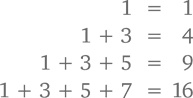

и предположили, что сумма первых n нечетных чисел равна n². Позже мы это подтвердили, причем очень красиво и остроумно – с помощью комбинаторного доказательства, подсчитав двумя разными способами количество клеток на шахматной доске. А почему бы нам не попробовать другой метод – пусть и не такой эффектный, но при этом ничуть не менее эффективный. Предположим, я сказал вам (или вы просто верите в то), что первые 10 нечетных чисел 1 + 3 +… + 19 дают в сумме 10² = 100. Если вы с этим согласны, значит, прибавление следующего нечетного числа – 21 – даст нам уже 121, что равно 11². Другими словами, если мое утверждение правдиво для десяти чисел, оно будет правдивым и для одиннадцатого. В этом и состоит суть математического доказательства по индукции: сначала мы доказываем, что некое утверждение относительно числа n является изначально верным (обычно при n = 1), а затем показываем, что, если это верно для n = k, оно останется автоматически верным для n = k + 1 и так далее – для любого значения n. Доказательство по индукции подобно подъему по лестнице: поднявшись на первую ступеньку, вы имеете все основания и все возможности подняться и на вторую. Ну а старая добрая логика настойчиво подсказывает, что так вы рано или поздно сможете оказаться и на пятой, и на десятой, и на n-ной ступени.

Так, в примере с первыми n нечетными числами наша задача – показать, что при любом значении n ≥ 1

Мы видим, что сумма самого первого нечетного числа – 1 – и в самом деле составляет 1², то есть для n = 1 наше предположение абсолютно верно. Дальше нам следует обратить внимание на то, что, если сумма первых k нечетных чисел составляет k², а именно

при добавлении следующего нечетного числа (2k + 1) у нас получится

Другими словами, если сумма первых k нечетных чисел равна k², то сумма первых k + 1 нечетных чисел обязательно будет равна (k + 1)². Значит, теорема, истинная в отношении n = 1, будет столь же истинной в отношении любого значения n.◻

Индукция – инструмент действенный. Эта книга начиналась с проблемы определения суммы первых n чисел. Разными путями мы пришли к тому, что

Это предположение, безусловно, правдиво при n = 1 (потому что 1 = 1(2)/2). Предположим, что оно правдиво и для числа k: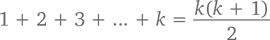

Тогда, прибавив к этой сумме (k + 1), получим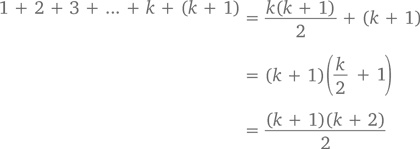

В этой формуле k + 1 использовано вместо n. Значит, если она верна для n = k (где под k может скрываться любое положительное число), она будет так же верна и для n = k + 1. Равно как и для любого положительного значения n.◻

В этой главе (да и в книге вообще) будет еще много примеров использования индуктивного метода. А пока для закрепления материала вот вам песня, написанная «музыкантами от математики» Дэйном Кэмпом и Ларри Лессером на мотив знаменитой «Blowin' in the Wind» Боба Дилана.