Мой метод. Руководство по воспитанию детей от 3 до 6 лет - читать онлайн книгу. Автор: Мария Монтессори cтр.№ 84

Разобравшись с арифметическими действиями до десяти, мы без труда переходим к аналогичным действиям с числами до двадцати. Небольшую сложность вызывают десятичные числа, требующие отдельных занятий.

В качестве дидактического материала мы используем картонные квадратные карточки, на которых крупно напечатано 10, а также набор картонных прямоугольников размером в половину квадрата, на которых напечатаны цифры от 1 до 9. Мы раскладываем эти цифры по порядку в одну линию: 1, 2, 3, 4, 5, 6, 7, 8, 9. Когда цифр уже не осталось, мы должны начать сначала и снова взять цифру 1. Эта цифра 1 как бы соответствует тому отрезку палочки десять, благодаря которому она становится длиннее палочки номер девять. Считая расположенные в виде лесенки палочки до девяти, мы видим, что осталась еще одна палочка, которую, за неимением других цифр, мы снова обозначаем цифрой 1. Но эта палочка гораздо длиннее первой; и, чтобы отличить ее от первой палочки номер один, мы ставим рядом с единицей нолик – то есть «ничего». Получается 10. Прикрывая ноль прямоугольными карточками с цифрами в порядке их возрастания, мы получаем: 11, 12, 13, 14, 15, 16, 17, 18, 19. Эти же числа получаются, если к палочке 10 мы сначала прибавим палочку 1, а затем палочку 2, палочку 3 и так далее, пока, наконец, мы не прибавим палочку 9, в результате чего получается очень длинная палочка, сосчитав красные и синие отрезки которой мы получим девятнадцать.

После этого учительница показывает ребенку карточку, например 16, и ребенок прикладывает палочку 6 к палочке 10. Потом она убирает карточку 6 и на ее место кладет карточку 8, и ребенок, соответственно, убирает палочку 6 и заменяет ее палочкой 8, получая, таким образом, 18.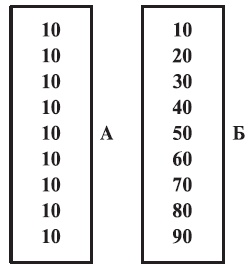

Каждое из этих действий можно записать следующим образом: 10 + 6 = 16; 10 + 8 = 18 и т. д. Точно так же мы учим детей вычитанию.

После того как ребенок получил ясное представление о числе, мы раскладываем прямоугольные карточки в два вертикальных ряда по девять карточек в каждом, как это показано на рисунках А и Б.

В столбике А мы закрываем нолик во второй десятке прямоугольником с цифрой 1; в третьей десятке мы закрываем его карточкой с цифрой 2 и т. д. Таким образом, единица слева остается без изменений, а числа справа возрастают от нуля до девяти.

В столбике Б процедура несколько сложнее. Здесь каждая последующая цифра больше предыдущей ровно на один десяток.

Почти все наши дети умеют считать до 100. Для них знакомство с этим числом – нечто вроде награды за проявленную любознательность.

Думаю, что дальнейшие объяснения по данному этапу обучения будут излишни. Любой учитель в состоянии разнообразить практические уроки арифметики, пользуясь простыми предметами, которые детям нетрудно складывать и делить на группы.

Используя наш метод на практике, очень важно знать и соблюдать последовательность описанных нами упражнений, с которыми детей нужно знакомить постепенно.

В первом издании моей книги я четко указывала на очередность каждого упражнения; но в доме ребенка мы сразу начали предлагать детям совершенно разные задания, что, в свою очередь, позволило нам говорить о наличии этапов в подаче всего материала, взятого как единое целое. По сравнению с первым изданием моей книги, описание каждого этапа стало более детальным, потому как теперь мы можем в полной мере опираться на опыт, приобретенный нами в доме ребенка.

Первый этап

Когда ребенок впервые переступает школьный порог, ему можно предложить следующие упражнения:

Бесшумная перестановка стульев (навыки повседневной жизни).

Шнуровка ботинок, застегивание пуговиц, крючков и т. д.

Цилиндры (упражнения на развитие сенсорики).

Одним из самих эффективных упражнений считается упражнение с цилиндрами (объемными вкладками). Благодаря ему ребенок учится фиксировать свое внимание на определенном предмете. Он впервые начинает сравнивать, выбирать, делать умозаключения. Все это способствует развитию умственных способностей.

Упражнения с объемными вкладками располагаются в порядке трудности следующим образом:

а) цилиндры, равные по высоте, но разные в диаметре;

б) цилиндры, отличающиеся друг от друга по всем параметрам;

в) цилиндры, отличающиеся друг от друга только весом.

Второй этап

Упражнения на развитие навыков повседневной жизни. Тихо вставать со своего места и так же тихо садиться. Пройти прямо по линии.

Упражнения на развитие чувств. Упражнения с предметами, разными по величине. Длинная лестница. Призмы или большая лестница. Кубики. Здесь ребенок выполняет упражнения на распознавание величины предмета. Эти задания похожи на предыдущие упражнения с цилиндрами, но выполняются совершенно в ином ключе. Предметы здесь гораздо больше по размеру. Различия между ними намного очевиднее, чем это было в предыдущих упражнениях, но в данном случае только зоркий взгляд ребенка подмечает эту разницу и выявляет допущенные ошибки. В предыдущих упражнениях сам дидактический материал был задуман таким образом, чтобы автоматически указывать ребенку на ошибку. Контроль достигался тем, что предметы могли быть расположены в строго определенном порядке, и никак иначе. И наконец, если в предыдущих упражнениях ребенок обычно совершал самые простые движения (он сидел за столиком и раскладывал мелкие предметы в определенном порядке), то на данном этапе ему приходится совершать более сложные движения, требующие порой небольших физических усилий. Ребенок должен опускаться на коврик, вставать на колени, подниматься, переносить достаточно тяжелые предметы и т. д.

Мы замечаем, что ребенок все еще продолжает путать два последних предмета в наборе, один из которых самый крупный, а другой – второй по величине. Даже научившись правильно располагать все остальные предметы, он еще долгое время не замечает своей ошибки. Это неудивительно: несмотря на то что каждый последующий предмет в наборе больше предыдущего на равную величину, эта разница становится все менее ощутимой по мере увеличения самих предметов. Например, маленький кубик, имеющий в основании 2 см, в два раза больше самого маленького кубика в наборе, у которого в основании всего 1 см, в то время как самый большой кубик с ребром в 10 см больше предыдущего (основание которого равно 9 см) всего на одну десятую сантиметра.

Таким образом, с точки зрения теории будет правильным начинать подобные упражнения с самых маленьких предметов. Занятие можно проводить с использованием материалов, знакомящих детей с понятиями величины и длины. Однако упражнение с кубиками, из которых мы выстраиваем «башню», для этой цели не подходит, ведь «башня» всегда должна иметь самый большой кубик в основании.