Имею скафандр - готов путешествовать! - читать онлайн книгу. Автор: Роберт Хайнлайн cтр.№ 31

Теперь к сути. По таблице, расстояние от Плутона до Солнца составляет 39 с половиной расстояний от Земли до Солнца. Однако у Плутона и Меркурия орбиты очень вытянуты. У Плутона расстояние до Солнца изменяется на два миллиарда миль, чокнуться можно. Больше, чем от Солнца до Урана. Плутон даже забирается внутрь орбиты Нептуна, а потом откатывается вдаль и маячит там пару столетий, совершая всего четыре оборота за тысячу лет.

Но в той статье говорилось, что на Плутоне начинается «лето». Значит, сейчас он находится вблизи орбиты Нептуна и будет находиться там до конца моей жизни — если бы я оставался в Кентервиле; здесь же предсказать, сколько я проживу, трудновато. В общем, получилась круглая цифра — 30 астрономических единиц.

Задачки на ускорение проще пареной репы: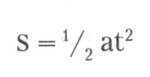

(расстояние равняется половине ускорения, умноженного на квадрат времени разгона). Если бы астронавигация этим и ограничивалась, любой новичок мог бы управлять космическим кораблем. Трудности происходят от гравитационных возмущений и того, что все движется одновременно и в четырнадцати разных направлениях. Однако я мог пренебречь гравитационными полями и движением планет. При скоростях, которые развивают корабли сколопендеров, эти факторы не имеют значения, если не подлетать слишком близко к планетам. Мне всего-то нужен был порядок величины.

Жаль, что нет логарифмической линейки. Папа говорит, что не умеющий ею пользоваться должен, как неграмотный, не допускаться до выборов. У меня прелесть, а не линейка — двадцатидюймовая, дуплексная, с тригонометрией от углов в радианах.

Папа осчастливил меня ей после того, как я освоил десятидюймовую, где все углы в градусах. Целую неделю пришлось сидеть на одной картошке, но папа заявил, что предметы роскоши в бюджете должны стоять на первом месте. Я знал, где сейчас эта линейка. Дома, на моем столе.

Ничего страшного. У меня есть цифры, формула, карандаш и бумага.

Прикинем. Жирный сказал «Плутон», «пять дней» и «восемь g».

Задача состоит из двух частей; половину времени (и расстояния) ускорение; потом разворот, вторую половину времени (и расстояния) — торможение. Полное расстояние нельзя использовать в уравнении, потому что время возводится в квадрат — функция параболическая.

В какой же конфигурации Плутон? В противостоянии? В соединении? В стоянии? Плутон в телескоп не видно — так кто помнит, в каком он месте эклиптики? Ну ладно, среднее расстояние 30 а.е.; отсюда будем танцевать.

Половина этого расстояния в футах равна: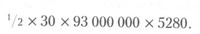

Восемь g равняются: 8 х 32,2 фута в секунду за секунду — скорость возрастает на 258 футов в секунду за каждую секунду до переворота, и с той же скоростью уменьшается после него. Таким образом из равенства: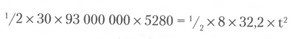

получаем время, за которое преодолеем половину пути, в секундах. Удваиваем его и получаем общее время в пути. Делим на 3600, получаем время в часах; делим на 24 и получаем дни. На логарифмической линейке такая задачка решается за сорок секунд, большую часть из которых потратишь на подсчет нулей. Элементарно, как подсчитать налог с продаж.

У меня ушел почти час на вычисления и почти столько же на проверку вычислений в ином порядке. Потом пришлось проверять еще раз, потому что результаты не совпали (я забыл умножить на 5280, и на одной стороне уравнения оказались футы, а на другой мили. Арифметика такого не любит. Потом я пересчитал все в четвертый раз, потому что уже ни в чем не был уверен. Все же логарифмическая линейка — лучшая штука в мире после девушек.

Наконец получился верный результат. Пять с половиной дней. Я на Плутоне.

Или на Нептуне…

Нет, на Нептуне я бы не смог подпрыгнуть на 12 футов; только Плутон отвечал всем условиям. Так что я все стер и высчитал, сколько придется лететь при одном g.

Пятнадцать дней.

Я-то думал, по крайней мере в восемь раз дольше, чем при восьми g — или даже даже в 64 раза дольше. Тут и крылась ошибка. Квадрат времени съедает преимущество в скорости — чем больше ускорение, тем короче путь, а чем короче путь, тем меньше времени ускоряешься. Чтобы сократить время вдвое, требуется четырехкратное ускорение; чтобы сократить время в четыре раза, ускорение нужно увеличить в шестнадцать раз, и так далее. Вот где была собака зарыта.

Сознание того, что я могу долететь до дома за две недели при ускорении в один g, подбодрило меня. За это время я не умру от голода. Если удастся украсть корабль. Если смогу им управлять. Если выберусь из этой норы. Если…

Не «если», а «когда»! В колледж я в этом году уже все равно не поступлю; плюс-минус пятнадцать дней никакой роли не играют.

Еще при первых расчетах я обратил внимание на максимальную скорость корабля перед разворотом. Более одиннадцати тысяч миль в секунду. Приличная скорость, даже по меркам космоса. Я призадумался. До ближайшей звезды, Проксимы Центавра, четырех и три десятых световых года, об этом то и дело слышишь в телевикторинах. Сколько займет путь при восьми g?

Задача та же, но надо следить за запятыми: числа становились громоздкими.

Световой год равен… я забыл. Придется умножить 186 000 миль в секунду (это скорость света) на количество секунд в году (365,25 х 24 х 3600) — получаем 5 880 000 000 000 миль. Умножаем на 4,3 и получаем 25 284 000 000 000 миль. Приблизительно 25 триллионов миль. Ничего себе!

А полет займет год и пять месяцев — короче, чем путешествие вокруг мыса Горн столетие назад.

Да эти чудища путешествовали между звездами!

Уж не знаю, почему я так удивился, ведь это просто в глаза бросалось. Я было принял как должное, что Сколопендер привез меня на свою родную планету, что он был плутонианцем, или плутократом, или как там еще. Но это было невозможно.

Он дышал воздухом. В его корабле для меня было достаточно тепло. Если он не торопился, то на небольшие расстояния путешествовал при ускорении, равном земному. Он пользовался освещением, которое подходило для моих глаз. Значит, он прилетел с планеты, похожей на мою.

Проксима Центавра — двойная звезда, как известно всем любителям кроссвордов. Одна из звезд — близнец нашего Солнца — размер, температура, другие свойства. Можно допустить, что у нее есть и планета, похожая на Землю? Я сильно заподозрил, что узнал домашний адрес Сколопендера.

И я точно знал, откуда они не могли прилететь. С планеты, которая веками несется в полном вакууме при температурах, близких к абсолютному нулю, где «летом» тают лишь газы, а вода остается твердой как камень, где даже Сколопендер вынужден носить скафандр. Они не могли явиться из Солнечной системы, потому что я был железно уверен, что Сколопендер нормально чувствует себя только на планете, похожей на нашу. Неважно, как он выглядит; пауки совсем не похожи на нас, но им нравится то же, что и нам. У нас, наверное, в каждом доме живет по тысяче пауков.