Лаборатория химических историй. От электрона до молекулярных машин - читать онлайн книгу. Автор: Михаил Левицкий cтр.№ 14

В химии довольно много устойчивых терминов, современная трактовка которых далека от первоначального смысла. Далее речь пойдет о термине "полидисперсность", известном далеко не каждому.

На бахче

Обычные арифметические задачи на проценты немного коварны. Если сумма имеющихся у вас денег уменьшилась на 20 %, а затем оставшаяся у вас сумма увеличилась на 20 %, то к прежней сумме вы не вернулись, и в конечном итоге денег у вас стало меньше. Немного неожиданно, но тем не менее все правильно: проведите простой расчет, взяв, например, исходную сумму 100 руб., и убедитесь, что все именно так.

Результаты некоторых задач на проценты очень удивляют. И вот пример: свежий арбуз, принесенный с бахчи, имеет массу 1 кг, и в нем 99 % воды. Естественно, настолько сильно "наводненных" арбузов не бывает, и цифры выбраны для простоты расчета. Арбуз выставили на солнце, часть воды из него испарилась, и теперь в нем 98 % воды. Какова теперь его масса? (Подсказка: в расчетах с помощью пропорции используйте «сухую» часть арбуза.) Ответ будет для вас неожиданным – он помещен в ссылку (рис. 1.46).

https://me-qr.com/1541214

Рис. 1.46.

Перейдем к выращенным арбузам. Предположим, что вы владеете небольшой арбузной бахчой и вам требуется оценить собранный урожай. Самое простое – пересчитать арбузы, но этот показатель малоинформативен, так как надо еще учесть их массу. Для простоты расчета масса каждого арбуза будет дана в килограммах, без дробных долей. Допустим, у вас 80 арбузов общей массой 640 кг, следовательно, средняя масса арбуза – 8 кг. Чем больше полученная цифра, тем успешнее у вас идут дела. Но есть еще дополнительная информация, которую можно представить наглядно. Построим диаграмму, где по горизонтальной оси будут указаны массы арбузов. Разделим все арбузы на группы, сложим в мешки, а для упрощения допустим, что внутри каждой группы арбузы имеют одинаковую массу. Изобразим эти группы (мешки с арбузами) на диаграмме в виде вертикально стоящих прямоугольников, и площадь прямоугольника будет равна количеству арбузов в этой группе. Получим диаграмму, показанную на рис. 1.47.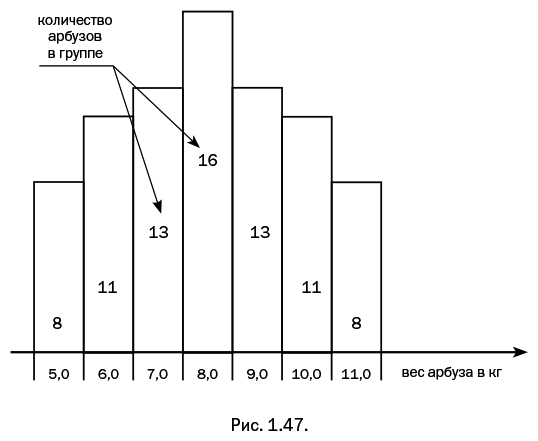

Для упрощения получившаяся пирамидка сделана симметричной, хотя правая и левая стороны у нее могли быть неодинаковы. Итак, мы вычислили среднюю массу арбуза – 8 кг, и это соответствует серединному прямоугольнику. Назовем эту величину среднечисленной массой, поскольку для расчета было использовано число имеющихся арбузов.

Так как мы уже рассортировали арбузы по массе и у нас имеется семь мешков (семь прямоугольников на диаграмме), вычислим среднюю массу арбуза другим способом. На диаграмме (рис. 1.48) показана та же пирамида, внутри каждого прямоугольника полужирным шрифтом выделена суммарная масса арбузов – то есть масса одного арбуза, умноженная на их число в этом мешке. Далее определим массовую долю каждого мешка, разделив его массу на общую массу – 640 кг. Полученные массовые доли указаны в прямоугольниках курсивом (рис. 1.48).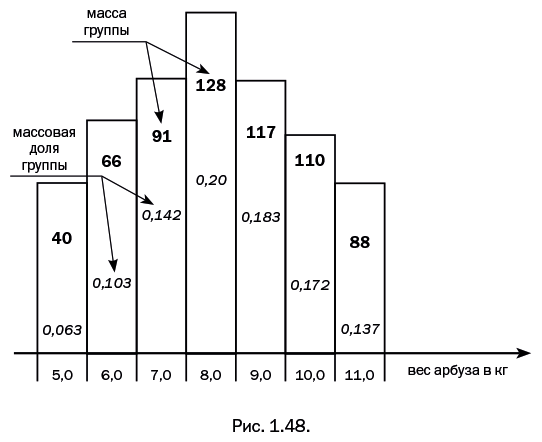

Естественно, сумма массовых долей всегда равна единице, 0,063+0,103+0,142+0,20+0,183+0,172+0,138 = 1. Для определения средней массы арбуза умножим массовую долю каждого мешка на массу находящегося в нем арбуза – и все просуммируем:

Назовем полученную среднюю массу арбуза среднемассовой, поскольку для расчета были использованы массовые доли. Эта величина немного больше полученной ранее среднечисленной массы (8 кг), что неудивительно – ведь эти величины вычисляли разными способами. Очевидно, что первый способ проще и логичнее. Потому невольно возникает вопрос: зачем нужен второй, совершенно головоломный способ? Ответ мы получим, рассмотрев урожай арбузов на соседней бахче (рис. 1.49).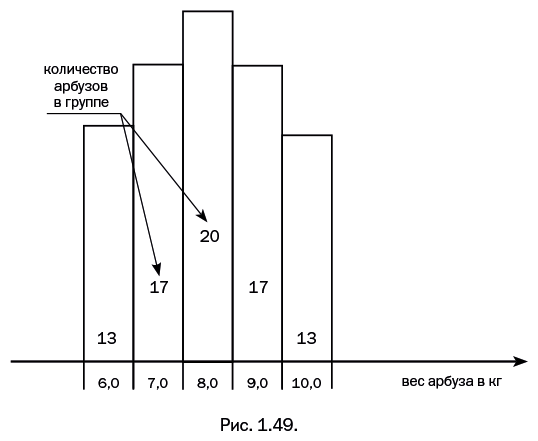

Результаты, полученные для собранного урожая на второй бахче, точно такие же, как и на первой: общая масса 13 · 6 + 17 · 7 + 20 · 8 + 17 · 9 + 13 · 10 = 640 кг. Среднечисленная масса одного арбуза 640 / (13+17+20+17+13) = 8 кг. Однако диаграмма второй бахчи внешне отличается от первой – она несколько ýже, то есть в массах арбузов меньший разброс. Такова визуальная картина, но как охарактеризовать это количественно? Нам может помочь среднемассовая величина. Если провести те же вычисления, что для первой бахчи, то для второй бахчи мы получим 8,3 кг. Мерой разброса арбузов по массе (то есть ширины диаграммы) может служить отношение среднемассовой величины к среднечисленной: на первой бахче 8,4/8 = 1,05, а на второй 8,3/8 = 1,04, то есть на второй бахче эта величина меньше. А какая бахча лучше? Оставим решать этот вопрос тем, кто выращивает арбузы, и двинемся дальше – теперь мы заменим арбузы полимерными молекулами.

Переходим к полимерам

Поскольку даже в крохотном образце полимера, взятом для исследования, содержится совершенно астрономическое число молекул, ступенчатая диаграмма, показанная на рис. 1.48, превратится в сплошную колоколообразную линию, называемую кривой молекулярно-массового распределения (рис. 1.50). Обычно она не симметрична, правая и левая ее ветви не одинаковы.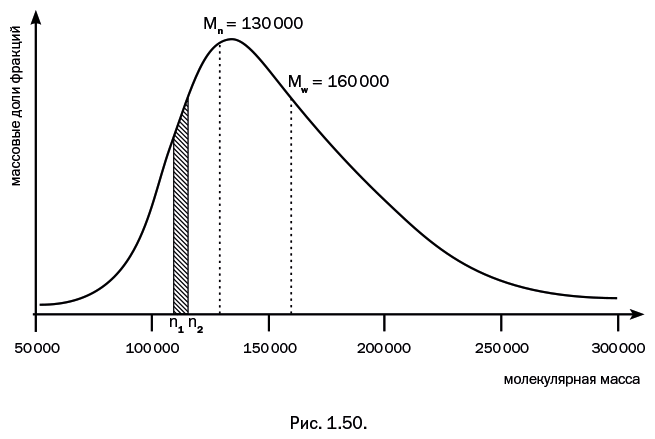

На рис. 1.50 показаны значения среднечисленной (обозначена M_n) и среднемассовой (обозначена M_w) молекулярных масс, которые имеют тот же смысл, что и в примере с арбузами. А ширина кривой, характеризующая степень разброса относительно среднего значения, точно так же вычисляется как M_w/M_n = 1,23. В полимерной химии ее называют полидисперсностью (от лат. dispersio – «рассеяние»). Площадь заштрихованного участка под кривой соответствует массовой доле той части полимера, которая имеет молекулярную массу в диапазоне n₁ – n₂, и это приблизительно соответствует мешку с арбузами одинаковой массы из предыдущей части рассказа. Такую часть полимера с молекулярной массой в небольшом диапазоне называют фракцией.

Существование у одного полимера двух значений молекулярной массы обычно удивляет синтетиков-органиков, которые точно знают, что индивидуальное вещество имеет строго определенную и только одну молекулярную массу, поскольку все молекулы одинаковы. В отличие от этого полимер – это смесь молекул различной величины. Два значения молекулярных масс являются не искусственно выдуманными – это результат того, что различные методы определения молекулярной массы дают разные значения. Среднечисленное значение дают методы измерения, более чувствительные к присутствию коротких молекул: например, криоскопия – понижение температуры замерзания раствора в сравнении с чистым растворителем – или эбулиоскопия – повышение температуры кипения раствора в сравнении с чистым растворителем.