
|
||
|
|
||
|
|
Онлайн книга - Математика жизни и смерти. 7 математических принципов, формирующих нашу жизнь | Автор книги - Кит Йейтс
Cтраница 63

Многие музыкальные стриминговые сервисы сегодня предлагают гораздо более сложные алгоритмы, чтобы разнообразить ваш плейлист. Если в последнее время вы часто слушали Beatles и Боба Дилана, генетический алгоритм может предложить вам попробовать группу, которая сочетает в себе некоторые характеристики этих двух исполнителей, – например, Traveling Wilburys (супергруппа Боба Дилана и Джорджа Харрисона). Пропуская песни или прослушивая их целиком, вы сигнализируете о том, насколько они вам подходят, давая алгоритму понять, из каких решений он должен исходить впредь. Плагины Netflix также предлагают вам случайные фильмы или сериалы, исходя из ваших предыдущих предпочтений. Недавно появилось множество компаний, советующих вам – при помощи похожих алгоритмов – разнообразить свой стол, посылая случайные подборки своих продуктов от сыров и вин до фруктов и овощей. Вы можете начать оптимизировать свой гастрономический опыт, исследуя вкусы, о существовании которых, возможно, даже не подозревали; при этом поставщики продуктов питания, ориентируясь на ваши отзывы, узнаю́т, что еще могут вам предложить. От моды до художественной литературы, компании используют инструменты эволюционных алгоритмов, настойчиво пытаясь разнообразить наш повседневный потребительский опыт. Время сказать: «Стоп!»
Возникает впечатление, что математическая основа некоторых рассмотренных выше алгоритмов оптимизации делает их исключительной прерогативой технологических гигантов, которые массово эксплуатируют эти алгоритмы в коммерческих целях. Однако существуют и более простые алгоритмы – хотя и в их основе лежит сложная математика, – с помощью которых можно вносить вроде бы мелкие, но очень существенные улучшения в нашу повседневную жизнь. Одно из таких семейств известно как «стратегии оптимальной остановки» и позволяет выбрать наилучший момент для вмешательства в процесс принятия решений. Предположим, например, что вы ищете, куда пригласить своего партнера на ужин. Вы оба очень голодны, но вы бы хотели, чтобы и место было приятным – первое попавшееся не подойдет. Вы считаете, что вполне способны оценить качество каждого ресторана по сравнению с другими. По вашим прикидкам, вы сможете проверить с десяток ресторанов, пока вашему партнеру не надоест шляться туда-сюда. При этом вы не хотите выглядеть нерешительным, поэтому не будете возвращаться в однажды отвергнутый ресторан. Лучшая стратегия для решения проблем такого рода заключается в том, чтобы посмотреть и сразу отвергнуть некоторые рестораны, чтобы почувствовать общую атмосферу. Вы можете просто выбрать первый ресторан, в который пришли, но, учитывая, что у вас нет абсолютно никакой информации, что это за заведение, есть только один шанс из десяти, что вы случайно выберете лучший. Так что стоит немного подождать и составить мнение о нескольких ресторанах, а потом выбрать первый из тех, что будет лучше, чем все те, в которые вы заходили прежде. Эта стратегия выбора ресторана проиллюстрирована на рис. 21. Первые три ресторана оцениваются, а затем отклоняются. Седьмой ресторан лучше всех предыдущих, поэтому на нем вы и останавливаетесь. Приятного аппетита! Но достаточно ли посетить три ресторана, чтобы получить надежные основания для отказа? Стратегия оптимальной остановки задается вопросом, сколько ресторанов нужно посмотреть и отклонить, чтобы получить представление о том, какой у вас выбор? Если посетите слишком мало ресторанов, вы не поймете, что предлагается к рассмотрению, но если вы исключите из списка слишком много, оставшийся выбор будет ограничен. 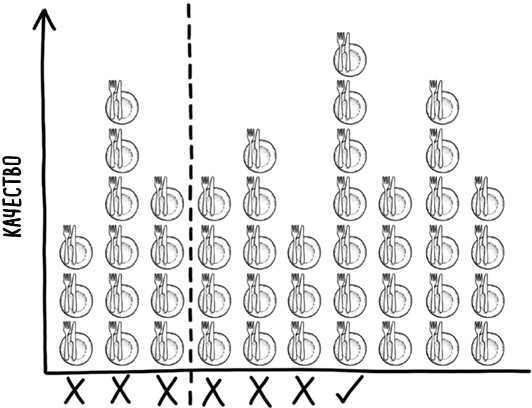
Рис. 21. Оптимальная стратегия заключается в том, чтобы оценить, но отклонить каждый вариант до заданной точки отсечения (пунктирной линии), а затем принять следующий оцениваемый вариант, который лучше всех предыдущих Математика, стоящая за этой проблемой, сложна, но оказывается, что следует оценить и отвергнуть примерно первые 37 % ресторанов (округленные до трех, если их всего 10), прежде чем выбрать следующий, который лучше всех предыдущих. Точнее, нужно отвергнуть 1/e долю всех доступных вариантов, где e – математическое обозначение числа Эйлера [158]. Число Эйлера составляет приблизительно 2,718, таким образом, 1/e – примерно 0,368 или, в процентном соотношении, 37 %. Рис. 22 иллюстрирует, как меняется вероятность выбора лучшего из 100 ресторанов по мере того, как вы варьируете количество ресторанов, которые отвергаете сразу. Если вы поспешите с решением, оно, по сути, сведется к слепому гаданию, поэтому неудивительно, что при слишком раннем выборе вероятность наткнуться на лучший ресторан низка. Аналогично, если вы выбираете слишком долго, то, скорее всего, вы уже пропустили лучший вариант. Вероятность наилучшего выбора максимальна, когда вы отклоняете первые 37 вариантов. 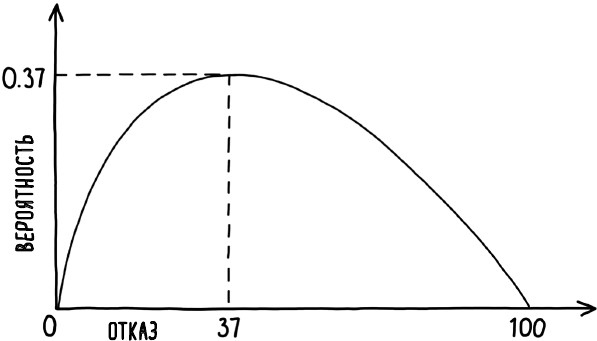
Рис. 22. Вероятность выбора наилучшего варианта максимальна, когда мы оцениваем и отклоняем 37 % вариантов, прежде чем принять следующий, который оценим выше, чем все, что видели прежде. В этом сценарии вероятность выбора лучшего ресторана составляет 0,37, или 37%
|
 Вернуться к просмотру книги
Вернуться к просмотру книги
 Перейти к Оглавлению
Перейти к Оглавлению
 Перейти к Примечанию
Перейти к Примечанию
 © 2020 LoveRead.ec - электронная библиотека в которой можно
© 2020 LoveRead.ec - электронная библиотека в которой можно