
|
||
|
|
||
|
|
Онлайн книга - Масштаб. Универсальные законы роста, инноваций, устойчивости и темпов жизни организмов, городов, экономических систем и компаний | Автор книги - Джеффри Уэст
Cтраница 42

Юнг знаменит не только своими исследованиями сердечно-сосудистой системы, но и несколькими другими разнообразными и глубокими открытиями. Наверное, более всего он известен созданием волновой теории света, согласно которой каждому цвету соответствует определенная длина волны. Но он также внес свой вклад в ранние работы по лингвистике и египетской иероглифике, первым расшифровав знаменитый Розеттский камень, хранящийся сейчас в Британском музее в Лондоне. Достойной данью уважения этому великому человеку стала вдохновенная биография Юнга, написанная Эндрю Робинсоном и озаглавленная «Последний человек, знавший все: Томас Юнг, незаметный ученый-универсал, который в числе других гениальных свершений доказал неправоту Ньютона, объяснил, как мы видим, излечивал больных, расшифровал Розеттский камень» [60]. Я питаю к Юнгу особую слабость, потому что он родился в городе Милвертоне в графстве Сомерсет на западе Англии, всего в нескольких милях от города Тонтона, в котором родился я. 12. Самоподобие и происхождение магического числа 4
В большинстве своем биологические сети, подобные системе кровообращения, проявляют одно любопытное геометрическое свойство: они фрактальны. Вы, вероятно, знакомы с этим понятием. Попросту говоря, фракталы – это объекты, которые выглядят приблизительно одинаково независимо от масштаба или степени увеличения. Классический пример фрактала – кочан цветной капусты или брокколи, изображенный на с. 149. Фракталы повсеместно распространены в природе и встречаются всюду, от легких и экосистем для городов, компаний, облаков и рек. Я хочу посвятить этот раздел разговору о том, что они собой представляют, что они означают, как они связаны со степенными законами масштабирования и как они проявляются в обсуждаемой системе кровообращения. Если головку брокколи разделить на меньшие части, каждая такая часть выглядит как уменьшенная копия исходной головки. При увеличении до размера целой головки кажется, что такую часть невозможно отличить от целого. Если каждую из этих частей также разделить на еще меньшие части, то и эти меньшие части будут выглядеть как уменьшенные копии исходной головки. Можно представить себе многократное повторение этой процедуры с практически одним и тем же результатом: каждая, все более мелкая, часть будет выглядеть как уменьшенная копия исходного целого. Говоря несколько другими словами, если сфотографировать любую часть брокколи и увеличить снимок до размеров исходной головки, отличить такую увеличенную фотографию от оригинала будет трудно. Такое положение вещей резко отличается от того, что мы привыкли видеть, например, когда мы смотрим на некий объект в микроскоп, используя все большее и большее увеличение, чтобы рассмотреть его более подробно и выявить новые структуры, качественно отличающиеся от целого. Очевидные примеры такой ситуации касаются, например, клеток в ткани, молекул в веществе или протонов в атоме. Однако если рассматриваемый объект – фрактал, увеличение разрешения не приводит к появлению никаких новых структур или деталей; вместо этого снова и снова повторяется та же самая структура. На самом деле это описание, конечно, идеализировано: изображения, получаемые с разным разрешением, несколько отличаются друг от друга, и в конце концов такое рекурсивное повторение прекращается, и появляются структуры новых типов. Если продолжать делить брокколи на все меньшие кусочки, рано или поздно они утратят геометрические характеристики головки брокколи, и можно будет увидеть структуру ее тканей, клеток и молекул. 
A) 
B) 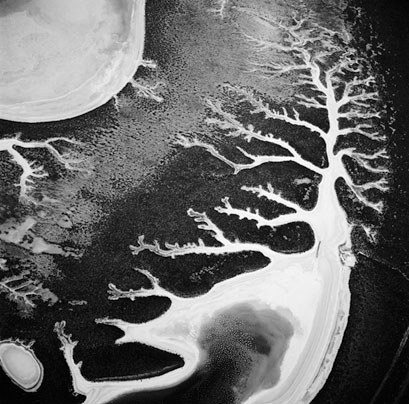
C) 
D) Примеры классических фракталов и масштабной инвариантности. Определение абсолютного масштаба во всех этих случаях затруднительно. A) и B): Два снимка капусты романеско, сделанные с разным разрешением, ясно показывают самоподобие. С) Русло пересохшей реки в Калифорнии. Очевидно сходство с зимним деревом, сухим листом или сосудистой системой человека. D) Большой каньон. Точно так же выглядит грунтовая дорога к моему дому, размытая после большой грозы Такое повторяющееся явление, называемое самоподобием, является общей характеристикой фракталов. Аналоги повторяющегося масштабирования брокколи можно найти в бесконечной последовательности отражений в параллельных зеркалах или в наборе помещающихся друг в друга матрешек все меньшего и меньшего размера. Задолго до изобретения этой концепции принцип самоподобия выразил в стихотворной форме ирландский сатирик Джонатан Свифт, автор «Путешествий Гулливера», написавший следующее ироническое четверостишие: Так, блох кусают маленькие блошки, А тех – свои, совсем, должно быть, крошки, Но и на них есть место паразитам… И так оно идет ad infinitum
[61]. Так же обстоит дело и с иерархическими сетями, о которых мы говорим. Если вырезать фрагмент сети и увеличить его до соответствующего размера, полученная сеть будет выглядеть в точности как исходная. Каждый уровень сети, по сути дела, образует локальную масштабированную копию смежных с ним уровней. Явный пример этой ситуации мы видели, когда говорили о последствиях согласования импедансов для пульсирующего режима работы системы кровообращения: ветвление с сохранением площади приводит к тому, что радиусы последовательно расположенных сосудов уменьшаются при каждом следующем разветвлении в постоянное число (√2 = 1,41…) раз. Поэтому, например, если сравнить радиусы сосудов, которые разделяет 10 таких разветвлений, их отношение будет равно (√2)10 = 32. Поскольку радиус нашей аорты равен приблизительно 1,5 см, это означает, что радиус сосуда, расположенного на десятом уровне ветвления, составляет всего около половины миллиметра.
|
 Вернуться к просмотру книги
Вернуться к просмотру книги
 Перейти к Оглавлению
Перейти к Оглавлению
 Перейти к Примечанию
Перейти к Примечанию
 © 2020 LoveRead.ec - электронная библиотека в которой можно
© 2020 LoveRead.ec - электронная библиотека в которой можно