Масштаб. Универсальные законы роста, инноваций, устойчивости и темпов жизни организмов, городов, экономических систем и компаний - читать онлайн книгу. Автор: Джеффри Уэст cтр.№ 100

Закон Ципфа назван по имени гарвардского лингвиста Джорджа Кингсли Ципфа, который популяризовал его в своей книге «Человеческое поведение и принцип наименьшего усилия», опубликованной в 1949 г. ^[131]. Впервые он сформулировал свой закон в 1935 г., в применении не к городам, а к частоте употребления слов в языках. В исходной формулировке этот закон утверждал, что частота появления любого слова в корпусе письменного текста, например в полном собрании пьес Шекспира или в Библии – или даже в этой книге, обратно пропорциональна его рейтингу в таблице частотности. Так, наиболее часто встречающееся слово используется приблизительно в два раза чаще, чем второе по частотности, в три раза чаще, чем третье, и так далее, как показано на рис. 40. Например, анализ текстов на английском языке показывает, что самое частое слово – это, что неудивительно, определенный артикль the, на долю которого приходится около 7 % всех используемых слов. Второе место занимает предлог родительного падежа of, частота появления которого приблизительно в два раза меньше и составляет около 3,5 % всех слов, а за ним следует союз and, частота употребления которого меньше приблизительно в три раза, а именно близка к 2,3 %, – и так далее ^[132].

Еще более загадочно то, что тот же самый закон оказывается справедливым для поразительно широкого спектра примеров, в который входят распределения по размерам морских судов, деревьев и элементарных частиц, метеоритов, нефтяных месторождений, файлов, передаваемых через интернет, и многого другого. На рис. 41 показано, как подчиняется этому закону распределение размеров компаний. Удивительная универсальность закона Ципфа и некоторые из его следствий привели к тому, что многие исследователи и авторы научных работ, воображение которых поразила его ошеломляющая простота, стали находить в нем некие мистические свойства. И сам Ципф, и многие последующие ученые размышляли о происхождении этого закона, но никакого общепринятого объяснения его существования так до сих пор и не появилось.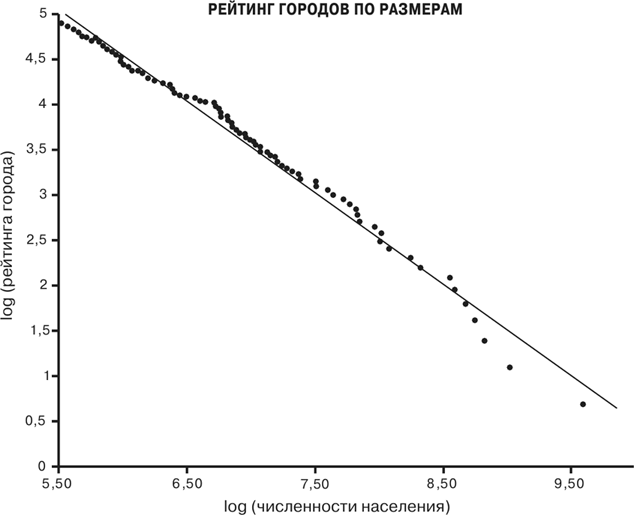

Рис. 39. Рейтинг городов США по размерам: по вертикальной оси отложен рейтинг городов, а по горизонтальной – численность их населения. Отметим, что на обоих графиках на этой странице имеются большие отклонения для точек с наибольшим рейтингом (слова the и города Нью-Йорка)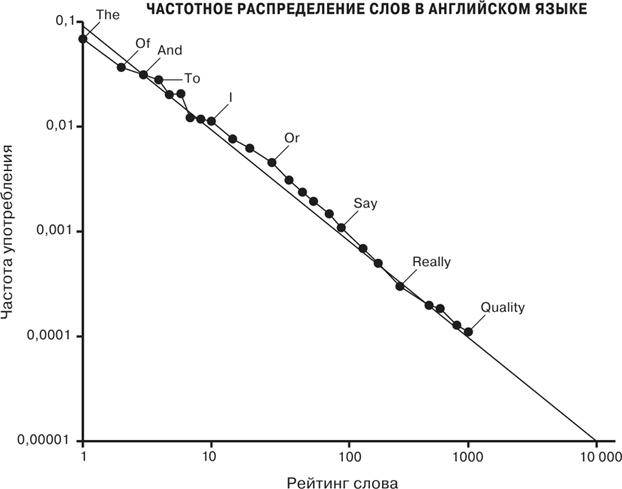

Рис. 40. Закон Ципфа для частотного распределения слов в английском языке: по вертикальной оси отложена частота употребления слов, а по горизонтальной – их рейтинг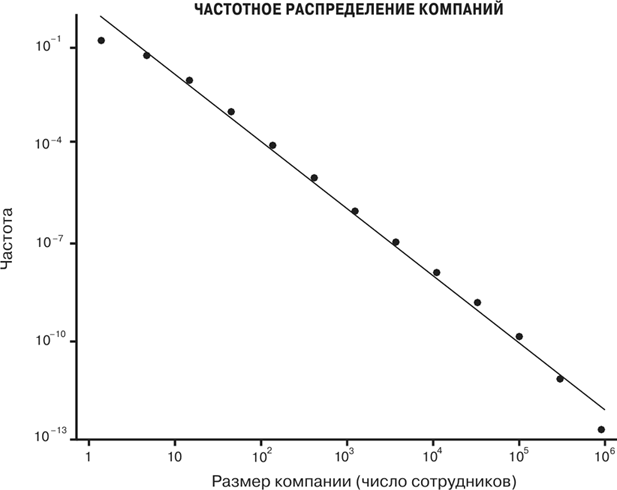

Рис. 41. Распределение американских компаний по размерам: по вертикальной оси отложен рейтинг компаний, а по горизонтальной – их размер (число сотрудников)

В экономике закон Ципфа появился на самом деле еще до Ципфа ^[133]. Он был открыт задолго до него авторитетным итальянским экономистом по имени Вильфредо Парето, который выразил его в виде частотного распределения доходов населения, а не их рейтингов. Это распределение, действующее для многих экономических параметров – например, уровня доходов, размеров состояний или величины компаний, – подчиняется простому степенному закону с показателем около –2. Если представить его в виде рейтинга, оно соответствует закону Ципфа. Оно выражает в численном виде тот вполне очевидный экономический факт, что существует крайне мало очень богатых людей или очень крупных организаций, но чрезвычайно много, соответственно, чрезвычайно бедных и чрезвычайно мелких. Закон Парето – или принцип Парето – зачастую сводят к так называемому правилу 80/20, согласно которому богатейшие 20 % населения получают 80 % суммарных доходов, что приблизительно соответствует действительности во всем мире. Аналогичным образом, примерно 80 % доходов компании поступают от 20 % ее клиентов, так же как и 80 % жалоб. Такая асимметричная ситуация, в которой существует лишь чрезвычайно малое число очень крупных образований и чрезвычайно большое число очень мелких, характерна для закона Ципфа. Например, чтобы понять 80 % литературы, требуется лишь около 20 % содержания словаря, а около 80 % населения проживает в 20 % крупнейших городов. Все точки, расположенные между этими крайними участками, приблизительно соответствуют обратно пропорциональной зависимости степенного закона.

Несмотря на общность «законов» Ципфа и Парето, часто встречаются и большие отклонения от них, и было бы наивно считать, что существует некий неизменный универсальный принцип, который точно определяет природу этих частотных определений, не рассматривая их в гораздо более широком контексте многих других динамических процессов. Например, одного лишь знания того, что размеры городов в городской системе следуют схеме Ципфа, вряд ли достаточно для разработки всеобъемлющей принципиальной теории городов. Как минимум, для этого требуется знание не только частотного распределения размеров, но и всех остальных законов масштабирования, о которых я уже говорил, описывающих весь спектр городской жизни, охватывающих в том числе потоки энергетических, материальных и информационных ресурсов. Хотя эти распределения и впрямь очень интересны, я склонен приписывать им гораздо более скромную роль, считая их лишь одним из множества феноменологических законов масштабирования, не обладающим каким-либо особым фундаментальным значением.