Мотивация человека - читать онлайн книгу. Автор: Дэвид Макклелланд cтр.№ 96

Типичные результаты, получаемые в исследованиях этой проблемы, представлены на рис. 7.1 и 7.2 (deCharms & Carpenter, 1968).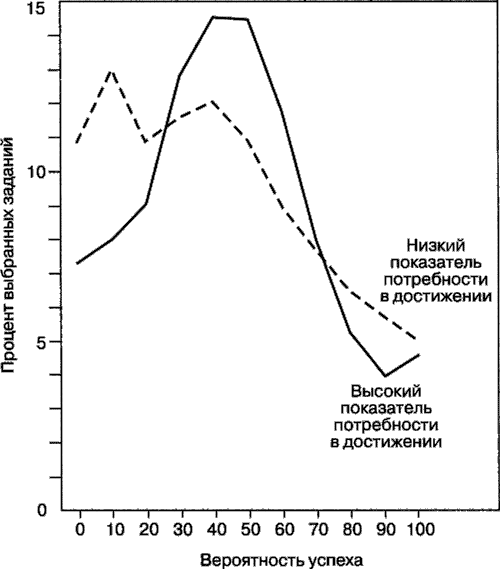

Рис. 7.1. Процент заданий каждого уровня вероятности успеха, выбранных при выполнении арифметических задач испытуемыми с показателем потребности в достижении выше и ниже медианы значений (по deCharms & Carpenter, 1968)

Испытуемыми были более 200 детей, учащихся 5-7-х классов городских школ. После того как дети выполнили стандартный тест для оценки потребности в достижении, им предложили ряд слов для проверки грамотности и ряд арифметических задач, которые были ранжированы по степени трудности: «После того как все дети попробовали выполнить все задания, им разъяснили различия в уровне трудности и каждому ребенку были сообщены его показатели успешности на каждом из уровней в соответствии с тем, сколько заданий каждого уровня он выполнил» (deCharms & Carpenter, 1968). Затем ученикам сказали, что они будут тестироваться индивидуально и смогут сами выбрать уровень трудности заданий, которые захотят решить. За правильное выполнение задания более высокого уровня трудности они получат больше баллов. Испытуемые знали, каковы их шансы на успех на выбираемом уровне трудности, поскольку могли посмотреть на свои прежние результаты, полученные на данном уровне. То есть на каждом уровне трудности предлагалось по 10 заданий, и если прежде они выполняли на этом уровне 2 задания, вероятность успешного выполнения составляла 2 из 10, или 0,20.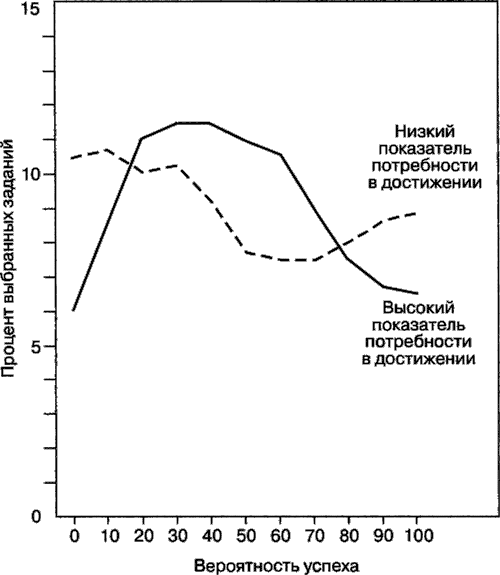

Рис. 7.2. Процент заданий каждого уровня вероятности успеха, выбранных при выполнении орфографических задач испытуемыми с показателем потребности в достижении выше и ниже медианы значений (по deCharms & Carpenter, 1968)

На рис. 7.1 и 7.2 показано, что испытуемые с выраженной потребностью в достижении обычно выбирали задания на уровне трудности со средней вероятностью успеха (от 0,30 до 0,50), тогда как испытуемые со слабо выраженной потребностью в достижении не обнаруживали подобных предпочтений. Если и проявлялись какие-то предпочтения, эти испытуемые были склонны выбирать очень трудные задания, где вероятность успеха была невелика (от 0 до 0,20). В случае орфографических заданий испытуемые со слабо выраженной потребностью в достижении были склонны выбирать очень простые слова, что обнаруживается и в других исследованиях (см. McClelland, 1958а).

Модель прогнозирования предпочтения умеренного риска Аткинсона

В своей классической работе Аткинсон (Atkinson, 1957) представил модель, объясняющую эти результаты. Он предположил, что сила тенденции к достижению при выполнении определенной задачи (или сила предпочтения в отношении разных задач) — это функция от мотива достижения, ожидания или вероятности успеха (P_s) и побудительной ценности успеха (I_s), где побудительная ценность успеха определяется как единица минус вероятность успеха (1 — P_s). Иными словами, предполагается, что ценность успеха прямо пропорциональна трудности его достижения. Как показано в табл. 7.2, при умеренной вероятности успеха, т. е. 50 на 50, произведение P_sxI_s максимально, что объясняет, почему умеренно трудные задачи обладают самой большой побудительной силой. Из табл. 7.2 также следует, что если мотив достижения (M_s) выше, как, например, при выраженной потребности в достижении, предпочтение умеренно трудных задач легким и чрезмерно трудным должно быть более выраженным (0,75: 0,27 по сравнению с 0,25:0,09). Рассматриваемая модель также предполагает, что даже лица со слабо выраженной потребностью в достижении должны отдавать предпочтение умеренно трудным задачам, что, однако, не соответствует действительности, как видно из рис. 7.1 и 7.2. Аткинсон разрешил эту проблему, предположив, что испытуемые со слабо выраженной потребностью в достижении в действительности боятся неудачи и склонны поэтому избегать задач умеренной степени трудности, т. е. отказываясь от этого предпочтения (см. главу 10).

Таблица 7.2

Активизированная тенденция достижения как функция от мотива достижения (М_S), ожидания или вероятности успеха (Р_S) и побудительной ценности успеха (I_S), где I₈ = 1 — Р_S(по Atkinson, 1957)

Задача	Низкий показатель потребности в достижении: MsxPsxIs = выбор задачи	Высокий показатель потребности в достижении: MsxPsxIs = выбор задачи
Задача А (трудная)	1x0,10x0,90 = 0,09	3x0,10x0,90 = 0,27
Задача Б	1x0,50x0,50 = 0,25	3x0,50x0,50 = 0,75
Задача В (легкая)	1 х 0,90x0,10 = 0,09	3x0,90x0,10 = 0,27

Модель Аткинсона, как уже говорилось, внесла определенную путаницу в терминологию, и ее необходимо разъяснить во избежание недоразумений. Иногда он называет произведение трех переменных, представленных в табл. 7.2, активизированной мотивацией к достижению, смешивая тем самым активизированную мотивацию достижения с тем, что мы назвали импульсом к действию (или выбору предпочтительной задачи), который является произведением мотивационных и немотивационных переменных и который Халл назвал потенциалом возбуждения (excitatory potential) (см. главу 3). Уровень мотивации достижения, активизированной в той или иной ситуации, можно определить, предъявив ТАТ в условиях активации (и сравнив полученный показатель потребности в достижении с этим показателем в нормальных условиях тестирования), однако Аткинсон не имел в виду (и не продемонстрировал), что измеренный таким образом уровень активизированной мотивации достижения является функцией от трех детерминантов, представленных в табл. 7.2. Он предполагал прогнозировать с помощью своей формулы тенденцию выбирать или активно работать над различными задачами, которую следует отличать от реально активизированной мотивации достижения, как это показано в мотивационной последовательности на рис. 6.1.

Как явствует из табл. 7.3, модель Аткинсона довольно убедительно объясняет реальное распределение выборов заданий разной степени трудности. Для ее проверки Литвин (Litwin, 1958) использовал игру в бросание колец, при которой выбор позиции на различном удалении от колышка отражал выбор уровня трудности задачи.

Таблица 7.3

Теоретическая и реальная привлекательность задач различной степени трудности в игре по бросанию колец (по Litwin, 1958)

Расстояние от колышкаа	Ценность		Вероятность успеха Ps		Побудительная ценность (прогнозируемая привлекательность, ценность х ожидание)		Соотношение
	Центы за попадание	Трудность (1 — Ps)	теоретическая	реальная	Центы х Ps	Трудность х Ps	Реальный выбор из 400
1-3	$0,04	0,01	0,99		0,04	0,01	0,00
4-6	0,14	0,12	0,88	0,70	0,12	0,11	0,05
7-9	0,29	0,30	0,70	0,31	0,20	0,21	0,09
10-12	0,50	0,45	0,55	0,20	0,27	0,25	0,33
13-15	0,62	0,62	0,38	0,15	0,24	0,24	0,34
16-18	0,81	0,75	0,25	0,14	0,20	0,19	0,18
а За минимальное расстояние было принято 10 дюймов [9] от колышка, последующие рубежи различались на 10 дюймов.