Вселенная. Емкие ответы на непостижимые вопросы - читать онлайн книгу. Автор: Мартин Дж. Рис, Питер Шварц, Роберт Дж. Сойер, и др. cтр.№ 19

Второй закон можно выразить и по-другому, сказав, что энтропии становится меньше и меньше по мере продвижения в прошлое. Таким образом, чем ближе мы подходим к Большому взрыву, тем меньше должна быть общая энтропия. Однако здесь появляется некий парадокс, по причине имевшего место в отдаленном прошлом чрезвычайно горячего состояния вселенной, которое мы определяем как Большой взрыв, чудовищно горячего состояния, выглядящего как тепловое, где слово «тепловой» обычно определяет максимальную энтропию! В самом деле, свидетельства, которые мы получаем, измеряя так называемый Космический микроволновый фон или CMB (электромагнитное излучение, приходящее к нам из космоса со всех направлений), по всей видимости, подтверждают это. Два наиболее явных и поразительных факта о CMB состоят, во-первых, в однородности во всех направлениях, которую он выявляет в структуре очень ранней вселенной, и во-вторых, в тепловой природе ее спектра (планковский спектр излучения). Оба они характерны для состояния максимальной энтропии! Это выглядит как выраженный парадокс, который мы обнаруживаем в этой очень ранней вселенной, состояние максимальной энтропии в этих двух аспектах, а именно однородности и планковском спектре. Не чрезвычайный ли это парадокс? Мы ведь должны были обнаружить состояние с очень небольшой энтропией, чтобы Второй закон оказывался верен и для самого начала существования вселенной.

Этот очевидный парадокс разрешается тем соображением, что наши предыдущие рассуждения включали только вещество и излучение в ранней вселенной, а роль гравитации не упоминалась. В отличие от случая вещества и излучения, где однородность означает высокую энтропию, в случае гравитации все наоборот. Если вы рассматриваете гравитацию, ситуации с низкой энтропией – то есть «высокоорганизованные» ситуации – это те, в которых геометрия очень, очень однородна.

По мере того как это однородно распределенное вещество начинает слипаться под воздействием гравитации, энтропия в гравитационном поле увеличивается. Слипшиеся области разогреваются и становятся звездами, а однородные области остаются холодными. Это проявление Второго закона термодинамики: резервуар с низкой (благодаря изначальной однородности) энтропией в гравитации в ходе гравитационного слипания переносится к объектам из концентрированного вещества, таким как звезды, вместе с более холодным межзвездным газом, где мы теперь видим дисбаланс температуры и плотности, который указывает на низкую энтропию в веществе. И от этого дисбаланса температуры зависит жизнь на Земле. Мы получаем энергию от Солнца в форме с низкой энтропией (относительно немного фотонов высокой энергии, где фотоны – квантованные элементы света), а ночью энергия возвращается в темное небо в форме с высокой энтропией (много-много фотонов низкой энергии). Таким образом растения с помощью фотосинтеза наращивают свою массу организованным низкоэнтропийным способом и поддерживают жизнь на этой планете. Все это происходит благодаря низкой энтропии в гравитационном поле, которое выражается в очень однородном начальном состоянии.

Одним из первых аргументов, выдвинутых в поддержку необходимости космической инфляции, было то, что раннее разглаженное состояние вселенной может быть объяснено, только если на очень ранней стадии ее существования произошло экспоненциальное расширение, которое разгладило бы любую неровность, которая могла бы возникнуть в самом начале. Этот аргумент и сейчас обычно приводят как причину для постулирования очень ранней инфляционной фазы. Однако именно этот аргумент в пользу космической инфляции, очевидно, неверен, поскольку требует от нее конфликтовать со Вторым законом термодинамики, волшебным образом уменьшая вклад гравитации в энтропию в ходе инфляционного расширения.

Этот контраргумент можно сделать более выразительным, если рассмотреть коллапсирующую модель вселенной – как нашу на рисунке 1, но с обратным направлением времени. С появлением небольших возмущений, развивающихся согласно Второму закону, этот коллапс ведет к огромной конгломерации сингулярных черных дыр, формирующихся на его финальных стадиях, и завершается невероятно сложной пространственно-временной сингулярностью, как показано на рисунке 4.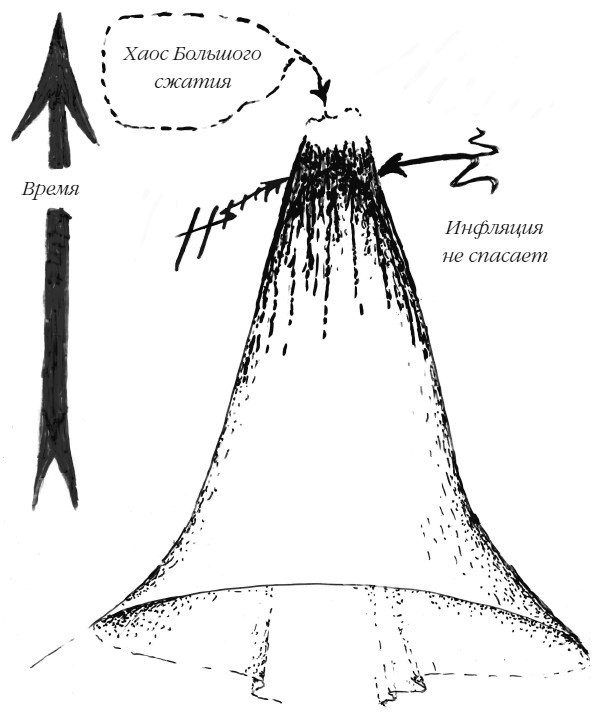

Рис. 4. Коллапс с образованием сложной пространственно-временной сингулярности.

На самом деле мы можем оценить, насколько более «вероятной» будет сингулярность на рисунке 4 по сравнению с рисунком 1, используя знаменитую формулу, называемую формулой Бекенштейна – Хокинга для энтропии черной дыры. Насколько более вероятным это будет? Ответ – примерно десять в степени 10¹²⁴ к 1, это 1000…00 к одному, где нулей – 10¹²⁴ штук. Это очень большое число! И это дает нам некоторое представление о том, насколько маловероятно, чтобы в конкретном случае произошел такой «Большой взрыв», как в нашей вселенной, или нечто подобное ему. Инфляция совершенно не уменьшает эту невероятность. Должно было быть что-то еще, что дало нам такой необычайно специфический начальный Большой взрыв.

Как нам определить этот особенный характер нашего Большого взрыва в элегантных геометрических терминах? Мой коллега по Оксфорду Пол Тод нашел очень элегантный способ выразить это математически – значительно улучшив способ, который предлагал я, – а именно, растянуть Большой взрыв наружу конформным образом, используя трюк, в основе своей противоположный тому, что мы использовали для бесконечности. То есть, модели вселенной, в которых гравитационная энтропия находится на своем минимуме, – это те, для которых Большой взрыв может быть конформно растянут до получения хорошей гладкой начальной поверхности. На рисунке 3 показаны оба эти конформных трюка; на нем видно, что не только будущая бесконечность сжата на гладкой конформной границе будущего, но и Большой взрыв растянут до хорошей гладкой конформной границы.

В этом нет ничего особенно необычного – просто пара милых математических трюков, призванных помочь нам размышлять об общей пространственно-временной геометрии вселенной. А теперь я сделаю кое-что очень необычное. Основная мысль здесь в том, что растянутый Большой взрыв и сжатая бесконечность – не просто конечные области. Растянутый Большой взрыв рассматривается как продолжение сжатой бесконечности предыдущего эона, и наша сжатая бесконечность продолжится Большим взрывом следующего эона. Я использую термин «эон» для описания фазы существования вселенной, начинающейся с Большого взрыва и становящейся бесконечным экспоненциальным расширением. Конформная бесконечность каждого эона меняет масштаб, становясь Большим взрывом следующего эона. Где-то в бесконечной череде эонов находится и наш эон, как это показано на рисунке 5. Получается бесконечная последовательность эонов до нашего и бесконечная последовательность эонов после нас. Это модель, которую я называю конформной циклической космологией, или КЦК.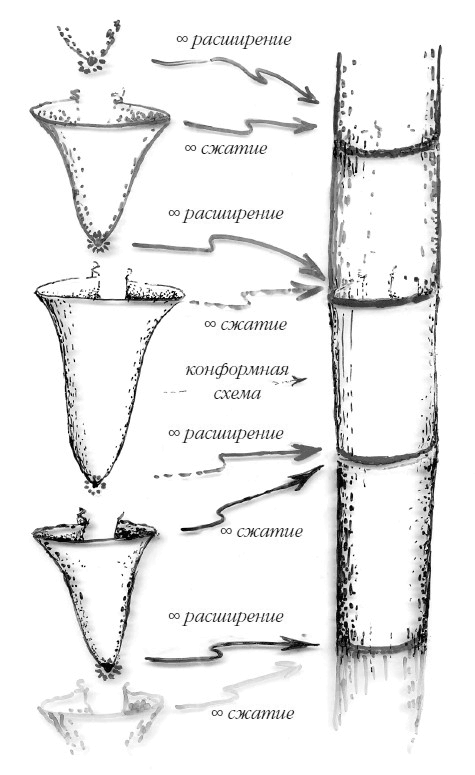

Рис. 5. Череда эонов.