Вселенная в вопросах и ответах - читать онлайн книгу. Автор: Владимир Сурдин cтр.№ 61

Обдумывая идею Майера, немецкий естествоиспытатель Герман Гельмгольц (Hermann von Helmholtz, 1821–1894) предположил, что на Солнце не обязательно должно что-то падать снаружи: «падать» на него может… вещество самого Солнца. Посмотрим еще раз на формулу для кинетической энергии (mv²/2): большой приток энергии обеспечивается либо высокой скоростью, либо большой массой. Поддержание высокой температуры звезды может происходить вследствие ее медленного сжатия. Сила тяготения при сжатии звезды совершает над газом работу, и это приводит к его нагреву. По расчетам английского физика Уильяма Томсона, барона Кельвина (William Thomson, 1st Baron Kelvin, 1824–1907), чтобы поддерживать свою светимость на современном уровне, Солнце должно ежегодно сжиматься всего на 90 метров, т. е. примерно на 1/15 000 000 долю своего радиуса. По оценке Томсона, сжимающееся Солнце могло светить не менее ярко, чем сегодня, на протяжении почти 30 млн лет.

Проверим это самостоятельным расчетом. Если ускорение силы свободного падения g = GM/R², то работа силы тяжести по перемещению массы m на расстояние h составляет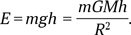

Если сжатие звезды происходит под действием собственной силы тяжести, то m = M и h ≈ R. Тогда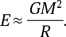

Это приблизительная оценка, но если вы умеете интегрировать, то можно доказать это точно. Гравитационная энергия тела, выделяющаяся при его сжатии от очень большого размера до радиуса R, составляет αGM²/R, где α — коэффициент порядка единицы, зависящий от распределения массы внутри тела.

Если сжатие происходит медленно, квазистатически, то в недрах звезды должно поддерживаться гидростатическое равновесие, а значит, по мере сжатия должны возрастать давление и температура. Несложно показать, что выделяющаяся при сжатии гравитационная энергия будет при этом делиться пополам: одна половина пойдет на нагрев недр звезды, а вторая — на излучение. Для знатоков теоретической механики сошлюсь на теорему о вириале. А для любителей небесной механики и космонавтики — на соотношение энергий у тел, движущихся с первой и второй космическими скоростями.

Приняв α = 1 (к большой ошибке это не приведет), получим характерное время излучения сжимающейся звезды t ≈ GM ²/(2RL), где L — светимость (т. е. мощность излучения) звезды. В честь Кельвина и Гельмгольца астрофизики называют эту величину временем Кельвина — Гельмгольца (t_KH). Для Солнца t_KH ≈ GM²_⊙/(2R_⊙L_⊙), где L_⊙ = 4 · 10²⁶ Вт, M_⊙= 2 · 10³⁰ кг и R_⊙ = 7 · 10⁸ м — светимость, масса и радиус Солнца. Подставляя эти значения в формулу, получим t_KH = 30 млн лет — в точности как у Кельвина! Это характерное время высвечивания Солнцем его гравитационной энергии связи.

Если у нас есть чувствительный детектор нейтрино, то мы заметим это сразу по прекращению потока солнечных нейтрино, рождающихся в термоядерных реакциях. Но не раньше чем через 8 мин 20 сек — времени, необходимого нейтрино, чтобы со скоростью близкой к световой долететь до Земли. Плюс время срабатывания самого детектора.

Если же у нас нет детектора нейтрино, то обычные астрономические наблюдения долго не позволят нам заметить выключение ядерного источника энергии Солнца, поскольку поддерживать его светимость будет другой источник — гравитационный (см. задачу «Солнце сжимается»). Размер Солнца при этом начнет уменьшаться. Современный угловой радиус Солнца около 15′ = 900″. Он существенно изменится за время Кельвина — Гельмгольца (см. задачу «Солнце сжимается») равное 30 млн лет. То есть скорость его изменения составляет примерно 900″/30 млн лет = 3 · 10^–5 угловой секунды в год. Если мы регулярно будем измерять радиус Солнца с точностью до 3″ (это типичное качество изображений на дневном небе), то сможем заметить его изменение лишь через 100 тысяч лет! Обычно размером солнечного диска интересуются астрономы, прогнозирующие и изучающие солнечные затмения. Они-то первыми и заметят уменьшение Солнца.

Кроме размера будет меняться и светимость Солнца, но медленнее, поскольку с уменьшением площади поверхности будет возрастать ее температура. Характерная скорость этого процесса также определяется временем Кельвина — Гельмгольца (30 млн лет). Наблюдаемые сейчас переменность солнечной светимости лежит в пределах 0,1 % и не сказывается на биосфере Земли. Однако расчеты показывают, что изменение светимости на 1 % приведет к изменению средней температуры Земли на 1÷2 K, что, вероятно, будет отмечено биосферой. Характерное время этого изменения не короче 300 тысяч лет.

Чтобы вода с Земли улетучилась в космос, ее надо нагреть до 100 °C, испарить и сообщить ее молекулам вторую космическую скорость. Теплоемкость воды — 4,2 кДж/(кг · K), а теплота ее испарения — 2256 кДж/кг. В глубине океанов вода холодная, так что нагреть ее придется от 0 °C до 100 °C. Полная работа по испарению килограмма воды составит 2676 кДж. А чтобы удалить молекулы в космос, нужно сообщить им 2-ю космическую скорость: V₂ = 11,2 км/с. Для удаления с Земли 1 кг чего угодно потребуется η = (1 кг) V²₂/2 = 6,27 · 10⁷ Дж. Это значение настолько больше теплоты нагревания и испарения воды, что только им и можно ограничиться.

Справочники подсказывают нам, что объем Мирового океана составляет 1340,74 млн км³, общий объем воды на планете — 1390 млн км³, а общая масса воды M = 1,46 · 10²¹ кг, что в 4000 раз меньше массы самой Земли. Светимость Солнца L_⊙ = 4 · 10²⁶ Вт. И у нас все готово, чтобы получить результат. Время испарения Мирового океана (или всей земной воды, что практически одно и то же) составит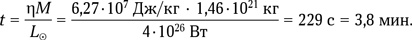

Иными словами, Солнце высушит Землю менее чем через 4 минуты.

Вычислить время полного разрушения Земли немного сложнее, поскольку по мере испарения ее внешних частей на поверхности оставшейся внутренней части будет меняться 2-я космическая скорость. Но, учитывая, что основная масса планеты лежит вблизи ее поверхности (благодаря росту площади шара как R²), ошибка будет невелика, если мы не станем учитывать этот факт. Тогда время полного испарения Земли будет в 4000 раз больше, чем время испарения воды (просто пропорционально их массам). Оно составит 10,6 суток. Полторы недели — и Земли нет. Вот на что способно наше Солнце. Хорошо, что оно этого не делает.