
|
||
|
|
||
|
|
Онлайн книга - Вселенная в вопросах и ответах | Автор книги - Владимир Сурдин
Cтраница 47

(знак минус говорит здесь о том, что направления векторов r и a противоположны). Как видим, это уравнение простых гармонических колебаний, возникающих в том случае, когда возвращающая сила пропорциональна отклонению тела от точки равновесия. В нашем случае эта точка — центр Земли. Решить это уравнение можно по аналогии с уравнением малых колебаний маятника: 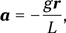
где g — ускорение свободного падения, L — длина маятника, r — его отклонение. Как известно, период колебания маятника составляет 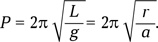
Значит, период колебания снаряда в шахте (независимо от амплитуды колебания!) составит 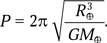
А полет между полюсами будет длиться 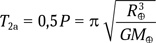
Таким образом, в случае однородной Земли снаряды прибудут к Южному полюсу одновременно (Т1 = Т2a). Однако известно, что к центру Земли плотность увеличивается, поэтому рассмотрим другой крайний случай. б) Пусть вся масса Земли сосредоточена в ее центре. Тогда ускорение снаряда 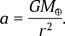
Это уравнение движения в поле точечной массы, типичное для тел Солнечной системы. Движение нашего снаряда по радиальной орбите можно представить как движение по вырожденному эллипсу с эксцентриситетом, практически равным единице. Тогда большая полуось этого эллипса равна R⊕/2, а орбитальный период 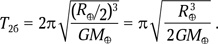
Это в
Задача решена. А теперь попробуйте рассмотреть третий вариант распределения плотности Земли — совершенно невероятный: пусть вся масса планеты сосредоточена в ее бесконечно тонкой оболочке, а внутри — пусто. Желаю успеха! 3.14. К антиподам разными путями
На снаряд, движущийся в плоскости экватора, будет (в системе отсчета, связанной с Землей) действовать центробежная сила, ослабляющая силу тяготения. Поэтому он пройдет через центр Земли позже и не столкнется с полярным снарядом, а на путь к антиподам затратит большее время. Полярный снаряд его опередит. 3.15. Связь между полюсами
Максимальную широту, на которой геостационарные спутники еще видны над горизонтом, определим из условия видимости объекта на горизонте 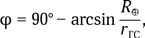
где rГС = 42 166 км — радиус орбиты геостационарного спутника. Приняв Землю за шар и взяв R⊕ = 6371 км, получим φ = 90° — 8,7° ≈ 81°. На более высоких широтах и тем более на полюсах Земли геостационарные спутники не видны с уровня моря. Значит, и связь с их помощью невозможна. 3.16. Маршрут по Луне
Кроме очевидного решения (южный полюс) существует еще бесконечное число таких точек в районе северного полюса, на расстоянии от него (35 + 20/2πn) км, при n = 1, 2, … 3.17. Посадка на Марс
Автор ошибочно привел значение скорости на низкой околоземной орбите, тогда как для Марса значение этой скорости существенно меньше — всего около 12 800 км/ч. 3.18. Летим на Солнце
Простейшее решение — после разрыва гравитационной связи с Землей развить скорость ее орбитального движения (около 30 км/с) в сторону, противоположную этому движению, т. е. «остановиться» на орбите и начать падать на Солнце по радиусу-вектору. Для этого вблизи Земли с учетом ее притяжения ракете необходимо развить скорость (мы помним, что сумма кинетических энергий — это сумма квадратов скоростей) 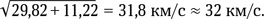
Заметим, что до такой скорости еще ни одна ракета не разгонялась. Поэтому более разумное решение — использовать для изменения скорости ракеты притяжение какой-либо планеты, совершив вблизи нее пертурбационный (гравитационный) маневр. Например, направив ракету к Юпитеру со скоростью около 16 км/с, можно таким образом рассчитать ее движение, что, сблизившись с планетой-гигантом, она изменит траекторию и упадет на Солнце. К сожалению, притяжения Марса для этого недостаточно. 3.19. Взлетаем
Пусть F — сила притяжения тела к Земле. Вес — это сила, с которой тело давит на опору. С такой же по величине силой опора давит на тело (третий закон Ньютона). Обозначим эту силу через F1. Вместе с ракетой тело движется вверх с ускорением g, и, следовательно, сумма F2 всех действующих на него сил равна mg (второй закон Ньютона). Положительным направлением мы выбрали направление движения ракеты, т. е. вверх. Поскольку F2 = F + F1, получим F1 = F2 − F, где F2 = mg и F = −mg. Отсюда F1 = 2mg. Таким образом, у поверхности Земли вес тела равен 2mg. С удалением от Земли сила притяжения F уменьшается, приближаясь к нулю (закон тяготения Ньютона). В предельном случае при F = 0 и F1 = F2 вес тела будет равен mg. Итак, вес тела убывает от 2mg у поверхности Земли до mg на бесконечности. |
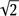 раз меньше, чем Т1 или Т2a. Очевидно, что истинное значение времени полета снаряда через шахту (Т2) удовлетворяет неравенству Т2a > Т2 > Т2б. Следовательно, Т2 < Т1, т. е. снаряд, отпущенный падать в шахту, достигнет противоположной точки Земли быстрее, чем снаряд, выведенный на орбиту. Как видим, это очень удобный вид межконтинентального транспорта и к тому же совершенно бесплатный (если не считать затрат на создание шахты и поддержания в ней вакуума!).
раз меньше, чем Т1 или Т2a. Очевидно, что истинное значение времени полета снаряда через шахту (Т2) удовлетворяет неравенству Т2a > Т2 > Т2б. Следовательно, Т2 < Т1, т. е. снаряд, отпущенный падать в шахту, достигнет противоположной точки Земли быстрее, чем снаряд, выведенный на орбиту. Как видим, это очень удобный вид межконтинентального транспорта и к тому же совершенно бесплатный (если не считать затрат на создание шахты и поддержания в ней вакуума!). Вернуться к просмотру книги
Вернуться к просмотру книги
 Перейти к Оглавлению
Перейти к Оглавлению
 © 2020 LoveRead.ec - электронная библиотека в которой можно
© 2020 LoveRead.ec - электронная библиотека в которой можно