
|
||
|
|
||
|
|
Онлайн книга - Вселенная в вопросах и ответах | Автор книги - Владимир Сурдин
Cтраница 38

0,61521 года × 13 = 7,998 года. То есть через 13 оборотов Венеры и 8 оборотов Земли они снова сходятся у того же узла орбиты Венеры. 3) В этом случае нам надо решить уравнение: 0,61521 года × (k + 0,5) = (n + 0,5) года, где k и n — целые числа, с точностью до 1/100. Приводим уравнение к виду 0,61521 k — 0,192395 = n и методом перебора находим пары (k = 171, n = 105) и (k = 197, n = 121). 1.30. Инспекция
Начальник станции был вежливый человек. Он согласился с замечанием и пообещал исправить оплошность. «Однако, — добавил он, — поскольку станция находится на свободно дрейфующей льдине, которую течением и ветром сносит иногда на несколько километров в сутки, отметку земной оси придется каждый день переставлять. Для этого понадобится дополнительная штатная единица, а также снегоход или вертолет и топливо». Руководитель комиссии замахал руками и сказал, что в смету эти расходы не заложены, дополнительных фондов нет и он не выделит на это ни копейки. Начальник станции пожалел, что такая хорошая идея не может быть реализована. «Бюджет — святое дело», — вздохнул он, и дискуссия о земной оси завершилась к обоюдному удовольствию. Мораль: учитесь разговаривать с чиновниками! 1.31. Эх, раз! Еще раз?
Как известно, звездные сутки длятся 23 часа 56 минут. Следовательно, в следующий раз звезда взойдет в 23:57 того же дня. Но между двумя восходами звезда должна пересечь линию горизонта при заходе. Следовательно, в течение текущих суток звезда появится на горизонте еще как минимум дважды. Но и это не предел! Звезда может проходить видимую (из данного места) часть своего пути очень низко над горизонтом, и тогда после второго восхода она еще может успеть сесть за оставшиеся до окончания суток три минуты. Поэтому полный ответ: звезда пересечет горизонт еще минимум 2, но, возможно, и 3 раза. 1.32. Замкнутый маршрут
Задача кажется очень легкой: искомая точка — Северный полюс. Но не торопитесь: существуют и другие решения. Кроме одной точки на Северном полюсе существует также бесконечное множество точек в окрестности Южного полюса, также удовлетворяющих условию задачи. Они лежат на концентрических окружностях с центром в Южном полюсе, имеющих радиусы Rk = 100 × (1 + 1/2 πk) км, где k = 1, 2, 3, … Например, при k = 1 мы выходим с расстояния около 116 км от полюса и, двигаясь на юг, приближаемся к нему до расстояния 16 км. Затем поворачиваем на восток и обходим вокруг полюса целый круг (длина окружности 2π · 16 = 100 км. Затем по уже пройденному пути возвращаемся на север в исходную точку. При k = 2 придется сделать два обхода вокруг полюса по кругу вдвое меньшего размера. При этом движение происходит все время строго на восток. Между расстояниями 116 и 100 км от Южного полюса заключено бесконечное число окружностей, все точки которых удовлетворяют условию задачи. 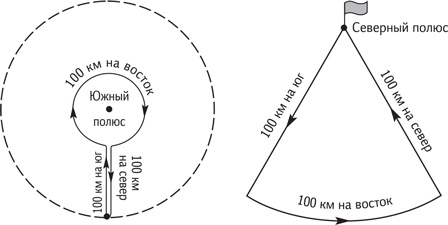
Решая эту задачу, мы считали поверхность Земли в районе полюса плоской, поскольку расстояния невелики. Но можно было бы учесть кривизну Земли. Это имело бы смысл, если бы в условии задачи был задан путь не 100 км, а 1000 км, 10 000 км, 20 000 км. Попробуйте решить эту задачу с такими условиями. Последнее из них особенно интересно. Землю мы считаем шаром с окружностью 40 000 км по экватору. 1.33. На все четыре стороны
Такие точки расположены на параллели, отстоящей на 5 км к югу от экватора. 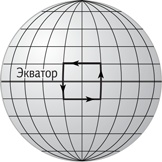
1.34. Небо вверх ногами
Перемещение наблюдателя из Восточного в Западное полушарие принципиально не меняет ориентацию созвездий относительно горизонта (это происходит только при существенном изменении широты, например при перемещении из Северного полушария в Южное). Тем не менее небольшое, но заметное даже для любителя астрономии изменение вида звездного неба при переезде из Москвы (широта около 56°) в Сан-Франциско (широта около 38°) все же происходит. 1.35. Что позади?
Позади фотографа — Солнце вблизи горизонта. 1.36. Зимний пейзаж
Судя по фазе Луны в виде тонкого месяца, она либо близка к новолунию, либо недавно прошла через него, т. е. расположена на небе недалеко от Солнца. Значит, это либо раннее утро перед восходом Солнца, либо ранний вечер, сразу после захода Солнца. Чтобы сделать однозначный выбор, нам нужно знать, в каком полушарии Земли находится эта местность. Если это Северное полушарие, то ориентация лунного серпа подсказывает, что на картине изображен вечер в средних широтах, если Южное — то утро в средних широтах. Однозначный выбор сделать невозможно. Однако общий вид пейзажа и строений на нем скорее соответствует Северному полушарию. Поэтому с большой вероятностью это вечер. О хорошей наблюдательности художника говорит тот факт, что он не забыл изобразить пепельный свет на темной стороне молодой Луны и правильно сориентировал «рога» лунного серпа, не направив их вниз (чем нередко грешат ненаблюдательные художники). Лунный серп у горизонта всегда имеет форму «лодочки», ориентированной «рогами» вверх и выпуклым «донышком» вниз, поскольку Солнце освещает Луну в этой фазе из-под горизонта. В экваториальных областях Земли «лодочка плывет» почти параллельно горизонту, в средних широтах — под наклоном, и чем ближе к полюсу, тем сильнее поднимается «нос лодочки» и опускается «корма». Но «лодочка» никогда не переворачивается. 1.37. Подзорная труба
Поскольку действие происходило практически на уровне моря, в трубу с любым увеличением поверхность моря видна не далее чем на 5–6 миль. На этом расстоянии проходит линия горизонта. Но если бы персонаж романа воскликнул: «Господа, миль на 100 квадратных вокруг не видно обломков кораблекрушения!», то он был бы прав: при R = 5,5 км площадь круга πR2 ≈ 100 км2.
2. Визит в обсерваторию
2.1. Темная сторона Луны
В момент солнечного затмения ночная сторона Луны освещена солнечным светом, отраженным дневной стороной Земли. Это слабое сияние называют «пепельным светом Луны». |

 Вернуться к просмотру книги
Вернуться к просмотру книги
 Перейти к Оглавлению
Перейти к Оглавлению
 © 2020 LoveRead.ec - электронная библиотека в которой можно
© 2020 LoveRead.ec - электронная библиотека в которой можно