Теория игр в комиксах - читать онлайн книгу. Автор: Айван Пастин, Тувана Пастин Пастин cтр.№ 6

Элис и Бэт – соседки по квартире. Им обеим нравится порядок на кухне, но ни одной не нравится порядок наводить. У каждой из девушек есть выбор: мыть посуду или не мыть. Таким образом, мы видим пример стратегического взаимодействия, так как счастье Элис (выигрыш) зависит от выбора действия Бэт, и наоборот.

Если ни одна из соседок не помоет посуду, выигрыш Элис составит 10 (А:10), так же как и выигрыш Бэт (Б:10). Эти показатели «счастья» используются нами просто для демонстрации предпочтительного для каждой девушки исхода. Если только Бэт помоет посуду, выигрыш Элис составит 20, однако выигрыш Бэт в таком случае уменьшится до 8 (А:20, Б:8). Если посуду помоет только Элис, получится обратная ситуация (А:8, Б:20). Если они приберутся вместе, то, поделив работу, выигрыш каждой девушки составит 14. И Бэт, и Элис понимают то, как их счастье зависит от исхода.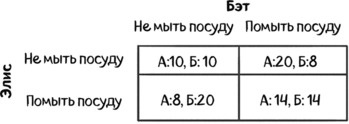

Равновесие Нэша достигается в случае, если ни одна из девушек не помоет посуду, то есть {не мыть посуду, не мыть посуду}, так как если каждая ожидает, что соседка не будет убираться, то наилучшим ответом будет бездействие.

В «Соседях по комнате» наблюдается так называемая проблема безбилетника. Выигрыш Элис является наибольшим, когда она отдыхает, пока Бэт моет посуду. Такая же ситуация возникает и у Бэт.

В равновесной ситуации ни одна из девушек не моет посуду, и выигрыш обеих составляет 10. Если бы они объединили свои усилия, то выигрыш каждой составил бы 14. Тем не менее чистота, достигнутая совместной работой, это не равновесный исход игры. Как только один из участников начинает ожидать, что порядок наведет другой, возникает стимул стать «безбилетником».

Из проблемы безбилетника существует выход: можно изменить выигрыши в матрице. Велико влияние родительского воспитания и школьного образования на человека – у него могут появиться угрызения совести при некооперативном поведении (например, когда он оставляет грязную посуду в раковине).

Изначально возникновение угрызений совести может показаться очень неудобным для соседок. Естественно, ведь никому не нравится чувствовать себя виноватым. Но при социальном взаимодействии угрызения совести могут подтолкнуть девушек к более кооперативному поведению и таким образом изменить равновесную ситуацию. Элис и Бэт получат бо́льшую выгоду, если будут следовать своим моральным установкам, так как они позволяют им достичь тех плодов сотрудничества, которые ранее были им недоступны.

Предположим, что за невыполнение своей части работы человека начнут мучить угрызения совести. Если одна из девушек не помоет посуду, ей будет стыдно, и ее счастье, обозначенное цифрой в матрице, уменьшится на 7. Равновесная ситуация будет достигнута при исходе {помыть посуду, помыть посуду}, а выигрыш каждой девушки составит 14.

Так как игроки решают объединиться, в равновесной ситуации совесть их мучить не будет. В таком исходе в связи с моральными установками участников будет наблюдаться улучшение по Парето. А их равновесные выигрыши вырастут с 10 до 14.

Международное сотрудничество в области защиты окружающей среды во многом похоже на игру «Соседи по квартире», только больше. Каждое государство предпочитает оставаться пассивным, пока другие страны внедряют дорогостоящие технологии, направленные на защиту природы и уменьшение выбросов углекислого газа. Решить этот вариант «проблемы безбилетника» можно было бы, подписав международное соглашение, которое обязывало бы государства платить денежные штрафы в случае, если выбросы углекислого газа в данной стране превышают установленный предел. Однако пока так и не удалось убедить страны, выбрасывающие в атмосферу наибольшее количество углекислого газа – США, Индия и Китай, – ратифицировать подобное международное соглашение.

Почему же так сложно подписать международное соглашение об ограничении вредных выбросов, ведь оно принесло бы всем столько пользы?

Сотрудничество принесло бы выгоду всем участникам, однако для США предпочтительнее всего было бы не подписывать соглашение о денежных штрафах, а оставить эту миссию другим странам. Ведь кто не любит прокатиться без билета?

С одной стороны, активная позиция относительно защиты окружающей среды означает усилия, направленные на изменение социальных норм. Те политики, что не поддерживают природоохранную политику, могут ощущать на себе давление. Это может изменить выигрыши лидеров государств точно так же, как угрызения совести девушек изменили их выигрыши в «Соседях по комнате». Такое политическое давление теоретически может привести к лучшему исходу, если оно создает равновесную ситуацию международного сотрудничества.

До сих пор мы рассматривали игры только с точки зрения равновесия Нэша. В тех играх равновесие Нэша делает один-единственный прогноз поведения игроков. Тем не менее люди часто сталкиваются с множеством равновесий Нэша. В играх с множеством равновесий концепция равновесия Нэша сама по себе не предоставляет нам достаточных средств для прогнозирования действий участников.

Какое же равновесие изберут участники игры с множеством равновесий?

В поисках ответа на этот вопрос американский экономист, профессор политической экономии и лауреат Нобелевской премии 2005 года Томас Шеллинг (1921–2016) пересмотрел суть экономики и ее место среди общественных наук.

Классическая игра «Битва полов» позволяет понять стимулы, возникающие в игре с множеством равновесий Нэша. Может показаться, что эта игра слишком проста и основывается на устаревших стереотипах, но она прекрасно иллюстрирует эту множественность, так как стимулы одной и той же формы проявляются в самых разных ситуациях.