Как работает мозг - читать онлайн книгу. Автор: Стивен Пинкер cтр.№ 92

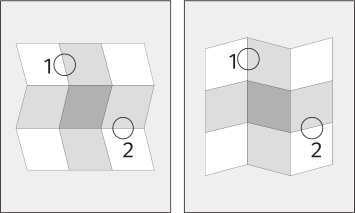
Стереоскопическое зрение – один из компонентов ключевого этапа зрительного восприятия, благодаря которому мозг определяет глубину и материал поверхности, но это не единственный его компонент. Чтобы видеть трехмерное изображение, не обязательно иметь два глаза. Достаточно полную информацию о форме и материале объекта можно извлечь даже из самых малозаметных особенностей изображения. Посмотрите на эти рисунки, которые придумал психолог Эдвард Адельсон ^[258].

Кажется, что на рисунке слева – белый кусок картона с серой вертикальной полосой, сложенный по горизонтали и освещенный сверху, а справа – кусок белого картона с серой горизонтальной полосой, сложенный по вертикали и освещенный сбоку. (Если смотреть на рисунок достаточно долго, любой из этих рисунков может перевернуться в трехмерном пространстве, как куб Неккера, но пока нас интересует не это.) Вместе с тем, штрихи, из которых состоят оба рисунка на странице книги (и проекции на сетчатке ваших глаз), примерно одинаковы. Каждый рисунок представляет собой зигзагообразную фигуру из клеток, некоторые из которых затенены. На обоих рисунках угловые клетки белые, верхние и боковые клетки – светло-серые, а средняя клетка – более темного оттенка серого. Каким-то образом сочетание затенения и зигзагообразное™ заставляет рисунки приобретать объемность и интенсивность окраски, но по-разному. Границы, помеченные цифрой «1», физически являются идентичными на обоих рисунках. Тем не менее на левом рисунке эта граница выглядит как изображенная краской (как белая полоска, нарисованная рядом с серой полоской), а на правом рисунке – как граница, созданная изменением формы и затенения (светлая полоска, переходящая в тень на другой стороне сгиба). Границы, помеченные цифрой «2», также идентичны друг другу, и здесь наблюдателю тоже кажется, что они различаются, только наоборот: на левом рисунке тень, а на правом – полоска из краски. Все эти различия происходят лишь от того, что в одном случае сгиб сделан вовнутрь в том месте, где во втором случае сгиб сделан наружу! Чтобы увидеть так много в таком маленьком изображении, нужно раскрыть три закона, благодаря которым в мире существует изображение. Для каждого закона нам понадобится «эксперт» внутри нашего мышления. Как и в случае со стереозрением, работа этих экспертов позволяет нам получить точное представление о поверхностях объектов, однако для этого они используют другие типы информации, решают другие типы проблем и делают другие типы предположений о мире.

* * *

Первая проблема – это перспектива: проекция трехмерного объекта в виде двухмерного силуэта на сетчатке. К сожалению, любая проекция может получиться от бесконечного количества разных объектов, и способа восстановить форму объекта только по его проекции не существует (в этом могли убедиться посетители комнат Эймса). Создается такое впечатление, что эволюция говорит нам: «Ну что ж, никто не идеален», а наш анализатор формы заставляет нас видеть наиболее вероятное состояние окружающего мира, исходя из одного изображения на сетчатке.

Как система зрительного восприятия умудряется рассчитать наименее вероятное состояние мира, руководствуясь этим изображением? Теория вероятности предлагает простой ответ: теорема Байеса, самый незамысловатый способ определения вероятности гипотезы, основанной на каких-либо фактах. Согласно теореме Байеса, вероятность того, что одна гипотеза предпочтительнее другой, можно определить по двум показателям для каждой гипотезы. Один из них – априорная вероятность: какова ваша степень уверенности в этой гипотезе до того, как вы рассмотрите факты? Второй – это правдоподобие: если бы гипотеза была истинна, какова была бы вероятность возникновения фактов в том виде, в котором мы их наблюдаем? Умножаем априорную вероятность гипотезы 1 на вероятность возникновения фактов при условии истинности гипотезы 1. Умножаем вероятность гипотезы 2 на вероятность возникновения фактов при условии истинности гипотезы 2. Возьмем отношение этих двух чисел и получим перевес в пользу первой гипотезы.

Каким образом наш анализатор трехмерного изображения использует теорему Байеса? Он делает ставку на тот объект, который с наибольшей степенью вероятности мог бы дать такие линии, если бы присутствовал в этот момент в окружающей обстановке местности, и который с большой степенью вероятности встречается в типичной обстановке. Перефразируя слова Эйнштейна о Боге, можно сказать: анализатор формы исходит из предположения о том, что мир хрупок, но не зол ^[259].

Итак, в анализатор формы должна быть заложена информация об определенных вероятностных показателях, связанных с проекцией (о том, какими объекты кажутся в перспективе) и с окружающим миром (какие в нем бывают объекты). Некоторые из вероятностных характеристик, связанных с проекцией, играют очень большую роль. Теоретически монетка может давать проекцию в форме тонкой линии, но такое бывает, только если смотреть на нее со стороны ребра. Если в обстановке перед вашими глазами есть монетка, какова вероятность того, что вы смотрите на нее со стороны ребра? Если кто-нибудь специально не сделал так, чтобы эти два условия были одновременно выполнены, вероятность не очень велика. При наблюдении с многих других точек зрения проекция монетки будет иметь форму эллипса. Анализатор формы исходит из посылки о том, что заданная точка зрения – обобщенная (а не выверенная с прицельной точностью для желаемого расположения предметов, как в одной из комнат Эймса), и делает соответствующие ставки. С другой стороны, спичка почти всегда дает проекцию в форме прямой линии, так что если на изображении есть линия, то при прочих равных условиях спичка будет гораздо более вероятным предположением, чем монетка.

Если на изображении не одна, а несколько линий, то угадать становится еще проще. Так, совокупность параллельных или почти параллельных линий редко бывает случайной. Непараллельные линии в мире редко дают почти параллельные линии в проекции: если бросить на пол пару спичек, они в большинстве случаев лягут под тупым или острым углом по отношению друг к другу. В то же время линии, которые являются параллельными в реальном мире – например, края телеграфного столба – почти всегда дают проекцию в виде почти параллельных линий. Следовательно, если на изображении есть почти параллельные линии, велика вероятность того, что в реальном мире им соответствуют параллельные друг другу края объекта. Существует еще много практических способов указать, какие формы объектов реального мира могут с большой долей вероятности дать те или иные элементы изображения в проекции. Маленькие Т-образные, У-образные, V-образные элементы, углы, стрелочки, параллельные закорючки – это проекции самых разных прямых краев, углов и симметричных форм. Художники-карикатуристы веками использовали эти правила, а наш хитрый анализатор форм может использовать их в обратном порядке, делая ставки на то, какие объекты находятся перед нашими глазами.