Как работает мозг - читать онлайн книгу. Автор: Стивен Пинкер cтр.№ 106

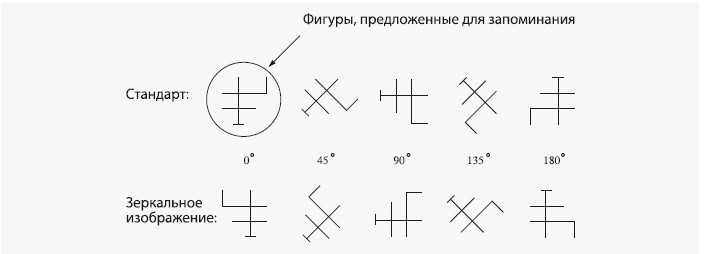
Если верить теории множества видов, люди должны были создавать отдельный файл в памяти для каждого положения, в котором объект появлялся на экране. Например, они должны были создать файл, изображающий, как фигура № 3 выглядит лежа на левом боку (а именно в таком виде они ее запоминали), а потом второй, изображающий, как она выглядит в положении на четыре часа, и третий – для положения на семь часов. Люди должны были вскоре научиться очень быстро распознавать фигуру № 3 во всех этих положениях. Когда мы затем неожиданно представили их вниманию те же фигуры, но в других положениях, они должны были думать немного дольше, потому что им необходимо было бы ввести новый вид в ряд уже знакомых видов, чтобы привести его в соответствие с остальными. На каждое из новых положений должно было потребоваться дополнительное время.

Если верить теории мысленного вращения, люди должны были быстро распознавать фигуру в вертикальном положении и все медленнее и медленнее – по мере ее отклонения от этого положения. Фигура, перевернутая вверх ногами, должна была занять больше всего времени, потому что для ее распознавания требуется поворот на все 180°; фигура в положении на четыре часа потребовала бы немного меньше времени, потому что для нее нужен поворот только в 120°, и т. д.

Если верить теории геонов, положение вообще не должно было иметь значения. Люди запомнили бы объекты, мысленно создавая описание каждой линии и пересечения в системе координат, привязанной к объекту. А когда на экране начали мелькать задания теста, для них было бы безразлично, как расположена фигура: на боку, с наклоном или вверх ногами. Наложение системы координат должно было быть быстрым и безошибочным, а описание фигуры относительно системы координат каждый раз совпадало бы с хранящейся в памяти моделью.

Конверт, пожалуйста. И победителем становится…

Все вышеперечисленное. Люди определенно хранят в памяти несколько видов каждой фигуры: когда фигура появлялась в одном из своих привычных положений, люди очень быстро ее идентифицировали.

Люди определенно вращают фигуры в уме. Когда фигура появлялась в новом, незнакомом положении, чем дальше ее нужно было поворачивать, чтобы совместить с наиболее близким к ней из знакомых видов, тем больше времени занимало у людей распознавание.

Наконец, – по крайней мере, для некоторых фигур – люди используют систему координат, привязанную к объекту, как в теории геонов. Мы с Тарром провели еще один вариант этого эксперимента, в котором использовались фигуры с более простой геометрией:

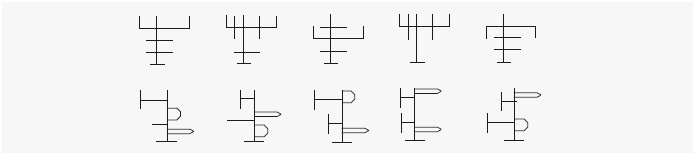
Фигуры были симметричны или почти симметричны, либо всегда имели одинаковые украшения с обеих сторон – так, чтобы людям никогда не приходилось описывать, как располагаются эти элементы по вертикальной или по горизонтальной оси в одной и той же системе координат. Что касается этих фигур, люди одинаково быстро узнавали их в любом положении, в положении вверх ногами – ничуть не медленнее, чем в правильном положении.

Итак, люди используют все эти приемы. Если левая и правая стороны фигуры не слишком различаются, они хранят ее в форме трехмерной геонной модели с центром в системе координат самого объекта. Если фигура более сложная, они хранят копию того, как она выглядит в каждом из положений, в котором они ее видели. Если фигура появляется в незнакомом положении, они мысленно вращают ее, совмещая с ближайшим из знакомых положений. Наверное, удивляться здесь нечему. Распознавание формы – это такая сложная задача, что единый универсальный алгоритм может просто не подходить для любой фигуры в любых условиях наблюдения.

Позвольте закончить эту историю самым радостным моментом для меня как для автора эксперимента. Вероятно, вы с недоверием восприняли эту идею мысленного вращения. Ведь все, что мы выяснили, – это что наклонные фигуры распознаются более медленно. Я поспешил сделать вывод, что люди вращают мысленный образ, но, может быть, наклонные формы просто сложнее анализировать по другим причинам? Есть ли доказательства того, что люди на самом деле осуществляют имитацию физического вращения в реальном времени, градус за градусом? Проявляются ли в их поведении хоть какие-то намеки на геометрию вращения, которые могли бы убедить нас, что они прокручивают в голове такое кино?

Мы с Тарром обнаружили кое-что, что нас поразило. Мы провели еще один эксперимент, в ходе которого протестировали людей на тех фигурах, которые они изучили, и на их зеркальных изображениях в разных положениях:

Это не был тест на распознавание зеркальных изображений, как в экспериментах Купера и Шепарда; людям сказали, что обе версии нужно рассматривать одинаково – точно так же, как мы используем одно и то же название для левой и для правой перчатки. Конечно, это естественная тенденция людей. Тем не менее наши испытуемые почему-то все равно воспринимали их иначе. Имея дело со стандартными версиями (верхний ряд), люди изучали их дольше, когда фигура была наклонена больше: каждая последующая картинка в верхнем ряду занимала у них немного больше времени, чем предыдущая. Однако когда речь шла о зеркальных версиях (нижний ряд), наклон не имел значения: на все положения затрачивалось примерно одинаковое время. Казалось, что люди осуществляют мысленное вращение стандартных фигур, но не делают этого с их зеркальными изображениями. Мы с Тарром были вынуждены написать статью, в которой уверяли читателя, что люди используют другую стратегию для распознавания зеркальных изображений. (В психологии объяснять непонятные данные с помощью «стратегий» – последнее средство, к которому прибегают, если не имеют понятия, что с ними делать.) Однако как раз в тот момент, когда мы уже готовили последний вариант рукописи к публикации, нас осенило.

Мы вспомнили теорему геометрии движения: двухмерную форму всегда можно совместить с ее зеркальным отображением путем вращения не более чем на 180°, при условии, что вращение происходит в третьем измерении вокруг оптимальной оси. Теоретически любую из наших зеркальных фигур можно было развернуть в глубину таким образом, чтобы она совпала со стандартной вертикальной формой, и на каждый такой разворот потребовалось бы одинаковое количество времени. Зеркальное изображение с наклоном в 0° просто развернулось бы вокруг вертикальной оси, как вращающаяся дверь. Перевернутая на 180° фигура могла бы повернуться, как цыпленок на вертеле. Фигура, лежащая на боку, могла бы развернуться вокруг диагональной оси примерно так: посмотрите на тыльную сторону правой руки, держа ее пальцами вверх; теперь посмотрите на свою ладонь, повернув ее пальцами влево. Для разворота других смещенных фигур могут служить различные наклонные оси; в каждом из этих случаев вращение составит ровно 180°. Это предположение идеально подошло бы для объяснения наших данных: возможно, люди мысленно вращали все фигуры, но действовали при этом оптимально – стандартные фигуры поворачивали по кругу в плоскости изображения, а зеркальные изображения поворачивали в глубину, выбирая наиболее подходящую ось для поворота.