Насосы интуиции и другие инструменты мышления - читать онлайн книгу. Автор: Дэниел К. Деннетт cтр.№ 30

упражнение 2

а. Напишите РПА-программу для этого графа потока. (Обратите внимание: поскольку программа разветвляется, вы можете пронумеровать шаги несколькими способами. Неважно, какой из них вы выберете: главное, чтобы на верные следующие шаги указывали команды безусловного перехода.)

б. Что происходит, когда программа пытается вычесть 3 из 3 или 4 из 4?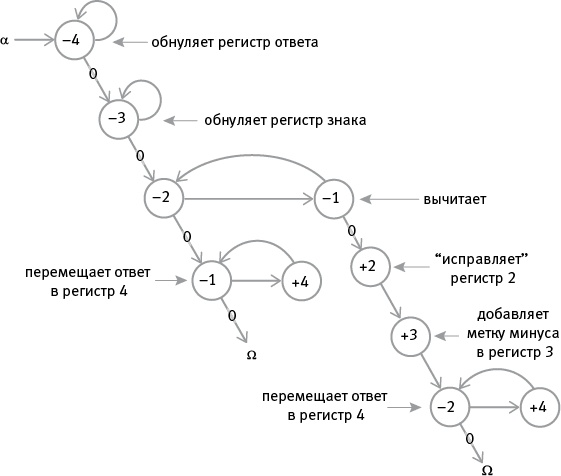

в. Какая возможная ошибка предотвращается обнулением регистра 3 перед попыткой вычитания на шаге 3 вместо шага 4?

Умея складывать и вычитать, мы легко можем разработать программы для умножения и деления. Чтобы умножить n на m, нужно просто прибавить n к самому себе m раз. Мы можем запрограммировать компьютер сделать это, используя один регистр как счетчик, который считает от m до 0, осуществляя одну операцию декрементирования по завершении каждого цикла сложения.

упражнение 3

а. Нарисуйте граф потока (и напишите РПА-программу) для умножения содержимого регистра 1 на содержимое регистра 3, поместив ответ в регистр 5.

б. (По желанию) ^[30] Используя копирование и перемещение, улучшите программу умножения, созданную в задаче а: когда она закончит работу, изначальное содержимое регистра 1 и регистра 3 восстановится, так что вы сможете легко проверить исходные данные и ответы на правильность по завершении программы.

в. (По желанию) Нарисуйте граф потока и напишите РПА-программу, которая изучает содержимое регистра 1 и регистра 3 (не разрушая их!) и записывает адрес (1 или 3) регистра с большим содержимым в регистр 2 или помещает 2 в регистр 2, если содержимое регистров 1 и 3 равно. (После выполнения этой программы содержимое регистра 1 и регистра 3 должно остаться неизменным, а регистр 2 должен показывать, равно ли их содержимое, а если нет, то в каком из регистров содержимое больше.)

Деление можно выполнять подобным образом, снова и снова вычитая делитель из делимого и считая, сколько раз мы можем провести эту операцию. Остаток – при наличии – можно поместить в специальный регистр для остатка. Но здесь обязательно нужно ввести важную меру предосторожности: на ноль делить нельзя (или можно?), поэтому перед началом деления необходимо провести простую проверку делителя, попробовав его декрементировать. Если его получилось декрементировать, нужно один раз его инкрементировать (чтобы восстановить его исходное значение), а затем провести деление. Если же в регистре ноль, после неудачной попытки декремента нужно поднять тревогу. Можно сделать это, зарезервировав регистр для метки ошибка: 1 в регистре 5 может означать “тревога! Меня только что попросили поделить на ноль!”.

Ниже представлен граф потока для деления содержимого регистра 1 на содержимое регистра 2, помещения ответа в регистр 3 и остатка в регистр 4 и резервирования регистра 5 для “сообщения об ошибке” (1 означает “меня попросили поделить на ноль”).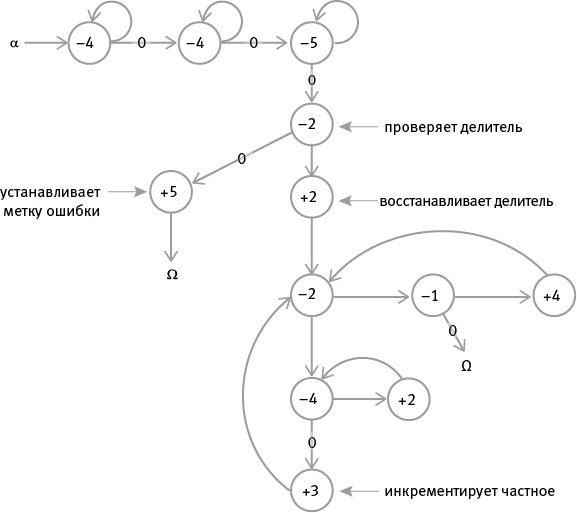

Изучите граф и обратите внимание, что ноль в делителе прерывает операцию и выдает сообщение об ошибке. Кроме того, заметьте, что регистр 4 служит двум целям: он не только выполняет роль копии делителя для восстановления делителя после каждой следующей операции вычитания, но и зарезервирован для потенциального остатка. Если регистр 1 обнуляется, прежде чем регистр 4 получает возможность вернуть свое содержимое обратно в регистр 2 для следующей операции вычитания, это содержимое и становится остатком, оказавшемся на своем месте.

Регистровая машина не тождественна сознанию. Она ничего не понимает, но вроде как понимает три простые вещи – Инк, Деп и Кон – в том смысле, что всякий раз слепо выполняет три этих “инструкции”. Само собой, это не настоящие инструкции, а лишь вроде как инструкции. Они кажутся нам инструкциями, и регистровая машина выполняет их так, как если бы они были инструкциями, так что нам более чем удобно называть их инструкциями.

Как вы теперь видите, эффективность регистровой машины объясняется существованием инструкции Деп, декремент-или-переход. Только эта инструкция позволяет компьютеру “замечать” (вроде как замечать) что-то в мире и использовать свои наблюдения для выбора следующего шага. Фактически существованием этой команды условного перехода объясняется эффективность всех компьютеров с хранимой в памяти программой, на что Ада Лавлейс обратила внимание еще в девятнадцатом веке, когда написала блестящий комментарий к описанию аналитической машины Чарльза Бэббиджа, которая стала прототипом всех компьютеров ^[31].

Когда вы наловчитесь собирать программы по частям, это станет для вас обычным делом. Однажды написав арифметические программы, мы можем использовать их снова и снова. Допустим, мы пронумеруем их: ADD станет операцией 0, SUBTRACT – операцией 1, MULTIPLY – операцией 2 и так далее. COPY может стать операцией 5, MOVE – операцией 6 и т. д. Теперь мы сможем использовать регистр, чтобы хранить в нем инструкцию, обозначая ее присвоенным номером.

упражнение 4 (по желанию)

Нарисуйте граф потока и напишите РПА-программу, которая превращает регистровую машину в простой карманный калькулятор, следующим образом:

а. Используйте регистр 2 для операции:

0 = ADD

1 = SUBTRACT

2 = MULTIPLY

3 = DIVIDE