Значимые фигуры - читать онлайн книгу. Автор: Йен Стюарт cтр.№ 10

Собственно термин «аль-джебр», который обычно переводят как «дополнение», относится к приему добавления одного и того же слагаемого к обеим частям уравнения с целью его упрощения. «Аль-мукабала», или «уравновешивание», относится к переносу одного из слагаемых с одной стороны уравнения на другую сторону (но с противоположным знаком) и к сокращению подобных членов в обеих частях уравнения.

К примеру, если уравнение в современной символьной записи выглядит как

то аль-джебра разрешает нам добавить по 3 к обеим сторонам уравнения и получить

что в данном случае решает уравнение. Если уравнение выглядит как

то аль-мукабала позволяет нам перенести 6 с левой стороны уравнения на правую, только со знаком минус, и получить

Вторая аль-мукабала позволяет нам перенести x² из правой части уравнения в левую и вычесть уже его, получив

что проще, но еще не дает решение уравнения.

Я повторю, что аль-Хорезми не использует никаких символов. Отец алгебры на самом деле не делал ничего из того, что сегодня большинство из нас считает алгеброй. Он все описывал словами. Конкретные числа были единицами, неизвестная величина, которую мы называем x, называлась у него корнем, а наш x² назывался квадратом. Приведенное уравнение в этих терминах выглядело бы так:

квадрат плюс корень равно двенадцать единиц,

и без всяких символов. Так что следующая задача – объяснить, как от уравнения подобного типа перейти к ответу. Аль-Хорезми подразделяет уравнения на шесть типов, причем типичный случай представляет собой «квадраты и корни равняются числам», то есть что-то вроде x² + x = 12.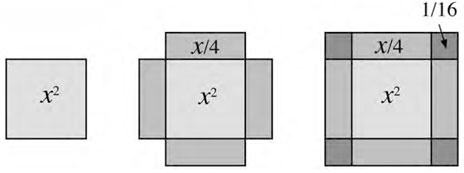

^{Геометрическое решение уравнений «квадраты и корни равняются числам»}

Затем он переходит к анализу каждого типа уравнений по очереди, причем решает их с использованием смеси алгебраических и геометрических методов. Так, чтобы решить уравнение x² + x = 12, аль-Хорезми рисует квадрат, который должен представлять x² (левый рисунок). Чтобы прибавить к этому корень x, он пририсовывает к квадрату четыре прямоугольника, каждый со сторонами x и 1/4 (средний рисунок). Получившаяся фигура наводит на мысль «завершить квадрат», присоединив сюда же четыре «уголка» – маленькие квадратики со стороной 1/4 и площадью 1/16. Так что он добавляет 4 × 1/16 = 1/4 к левой части уравнения (правый рисунок). По правилу аль-джебр он должен также прибавить 1/4 и к правой части уравнения то, в результате чего справа становится 12 1/4. Теперь

(x + 1/2)² = 12 1/4 = 49/4 = (7/2)².

Извлечем квадратный корень из обеих частей уравнения и получим

x + 1/2 = 7/2,

так что x = 3. Сегодня мы взяли бы еще отрицательный квадратный корень, -7/2, и получили второе решение, x = –4. Отрицательные числа уже начинали появляться в трудах ученых периода аль-Хорезми, но сам он их не упоминает.

Такой подход был бы понятен и вавилонянам, и грекам, поскольку они и сами в свое время занимались примерно тем же. На самом деле существуют сомнения относительно того, был ли аль-Хорезми знаком с «Началами» Евклида. По идее, должен был быть знаком, поскольку аль-Хаджжадж – другой ученый из «Дома мудрости» – перевел Евклида на арабский, когда аль-Хорезми был молодым человеком. Но с другой стороны, основной задачей «Дома мудрости» был именно перевод, и его работники не были обязаны читать труды, переведенные их коллегами. Некоторые историки утверждают, что геометрия аль-Хорезми по стилю не соответствует Евклидовой, и это свидетельствует о том, что ученый не был знаком с оригиналом. Но, я повторяю, «Алгебра» – популярная книга о математике, так что она и не должна была бы следовать аксиоматическому стилю Евклида, даже если бы сам аль-Хорезми знал Евклида назубок. Во всяком случае идея достраивания квадрата восходит еще к вавилонянам и позаимствовать ее можно было из множества разных источников.

Почему же тогда многие историки считают именно аль-Хорезми отцом алгебры? Особенно с учетом того, что он не использует никаких символов? И у него имеется сильный конкурент, грек Диофант. В его «Арифметике» – серии книг о решении уравнений в натуральных или рациональных числах, написанной около 250 г., – символы используются. Один из ответов состоит в том, что главной областью интересов Диофанта была теория чисел да и символы его были, по существу, простыми сокращениями. Однако более глубокий ответ, который мне кажется и более убедительным, заключается в том, что аль-Хорезми часто, хотя и не всегда, приводит универсальные методы решения, тогда как его предшественники, как правило, брали пример с конкретными числами и решали его. Читателю оставалось самому выводить общее правило. Так что результат приведенного выше геометрического решения мог бы выглядеть примерно так: «Возьмите 1, поделите на 2, получится 1/2. возведите ее в квадрат, получится 1/4, затем добавьте по 1/4 к каждой стороне», – и читатель должен будет сам догадаться, что общее правило состоит в том, чтобы заменить первоначальную 1 половинкой коэффициента при x, возвести результат в квадрат, прибавить результат к обеим сторонам уравнения и т. д. Конечно, при обучении преподаватель разъяснил бы решение на таком уровне обобщения и закрепил результат, заставив ученика прорешать множество других примеров.

Иногда аль-Хорезми, кажется, делает ровно то же самое, но, как правило, он подробнее описывает применяемые правила. Так что более глубокая причина того, что именно ему приписывают изобретение алгебры, состоит в том, что он сосредоточился на общих правилах манипулирования алгебраическими выражениями, нежели на конкретных числах, которые они представляют. К примеру, он дает правила раскрытия скобок при их перемножении

в терминах квадрата x², корня x и чисел. Мы бы записали это правило символически как

и именно это он говорит, словесно, без использования конкретных чисел для a, b, c или d. Он рассказывает читателям, как нужно манипулировать общими выражениями в числах, корнях и квадратах. Эти выражения рассматриваются не как зашифрованные версии какого-то неизвестного числа, но как новый тип математического объекта, выражения с которым можно просчитывать, даже если реальные числа вам неизвестны. Именно этот шаг к абстракции – если мы примем его как таковой – лежит в основе утверждения о том, что аль-Хорезми изобрел алгебру. В «Арифметике» ничего подобного нет.