Самая большая ошибка Эйнштейна - читать онлайн книгу. Автор: Дэвид Боданис cтр.№ 18

Принцип работы этих математических инструментов основывался на том, что давно осознали картографы, бороздившие планету, измеряя долготы и широты. Когда топографы и геодезисты XVIII века делали промеры между деревянными вехами, разделенными десятками миль, то (даже если земля между ними казалась просто пустынной равниной, сплошь засыпанной снегом и совершенно плоской) по угловым параметрам они могли установить, насколько в действительности искривлена поверхность между этими пунктами.

На плоской равнине любые огромные прямоугольники из таких геодезических вех обладали бы действительно прямыми углами – ровно в 90° каждый. А вот на гораздо более искривленной поверхности такие прямоугольники «вспухали» бы, так что их углы превышали бы 90°.

Поверхность Земли, чья сравнительно незначительная кривизна не позволяет путешественникам обнаружить эту кривизну невооруженным глазом, способна порождать удивительные эффекты. Вообразим, к примеру, что от Финляндии до Северного полюса простирается совершенно гладкая ледяная равнина. Двух конькобежцев из маленького финского городка расставляют в одной-двух милях друг от друга, а затем по сигналу оба начинают скольжение на север по абсолютно прямым линиям.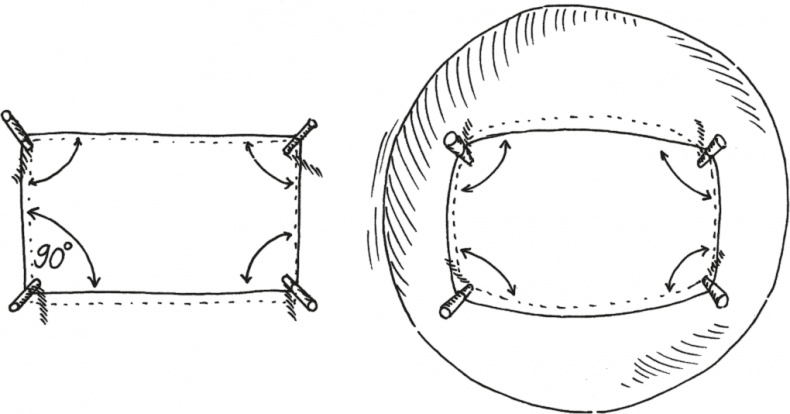

Вначале им кажется, что это легко. Из своего опыта катания по плоским замерзшим озерам родных краев они знают, что два конькобежца, начинающие двигаться параллельно, могут, казалось бы, скользить так сколько угодно.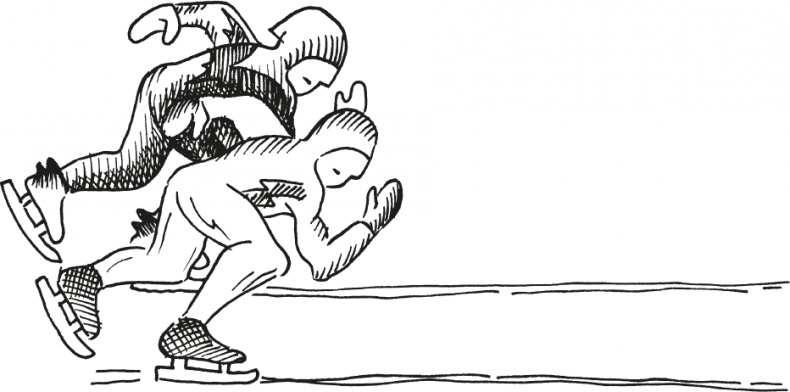

Теперь же, по мере того, как они все больше удаляются от дома, прилежно и неутомимо следуя полученным инструкциям, постоянно сверяясь с компасом и стараясь не отклониться вбок ни на один дюйм, они с удивлением замечают, как что-то «тянет» их друг к другу по мере того, как они все больше приближаются к полюсу, пока на «макушке» планеты они попросту не врежутся друг в друга.

С их точки зрения это необъяснимо. Почему два спортсмена, начавшие свой путь в милях друг от друга и старательно придерживавшиеся параллельных курсов, в конце концов столкнулись? Как такое могло получиться? Но если взглянуть на них с достаточной высоты (скажем, с гигантского воздушного шара, откуда открывается вид на эти две фигурки, упорно скользящие по льду), ответ станет ясен. То, что конькобежцы ощущают как неотвратимое тяготение, влекущее их друг к другу, на самом деле вовсе не проявление какой-то таинственной силы. Наша планета – это, грубо говоря, шар. Поэтому движение по таким вот параллельным прямым линиям, мысленно пролагаемым по поверхности этой сферы, неизбежно приведет к тому, что наши конькобежцы рано или поздно столкнутся.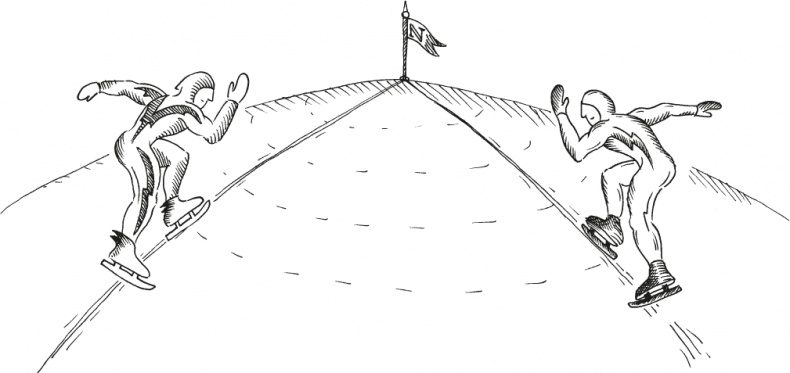

Именно такое явление Эйнштейн и вообразил себе в рамках своего мысленного эксперимента с таинственно сближающимися яблоками (просто нам кажется, что история с яблоками происходит не на плоскости). Однако в ту пору мало кто верил, что подобные причудливые эффекты и искривленные пути могут существовать (или, по крайней мере, иметь практическое применение) вне поверхности нашей планеты: иными словами, что космическое пространство, которое кажется нам пустым, на самом деле может обладать какой-то скрытой структурой, способной оказывать влияние на движущиеся в нем объекты. Напротив, все полагали, что само пространство, где находятся звезды и планеты, полностью соответствует представлениям Ньютона: это пустынная и довольно скучная штука, темная голая сцена, куда пока не вышли актеры.

Теперь же Гроссман объяснил Эйнштейну, что некоторые математики представляют отрадное исключение в этом хоре единообразия мнений. Еще за несколько десятилетий до того, как Эбботт написал свою сказку о Флатландии, они уже предположили: а не существует ли наша планета в рамках какой-то более обширной геометрии, нежели та, что доступна нашему непосредственному восприятию? Венгерскому офицеру Яношу Бойяи эта идея показалась столь заманчивой, что, перебрав кое-какие ее логические следствия, он (как сам Бойяи писал в 1820 году) почувствовал, что «создал новую вселенную из ничего!». Немецкий математик Карл Фридрих Гаусс, хоть и занимался вполне академической наукой, то и дело обращался к таким идеям на протяжении десятилетий и отмечал, что «теоремы [из области криволинейной геометрии] кажутся парадоксальными, а непосвященным – даже абсурдными, однако взвешенное и неуклонное размышление позволяет обнаружить, что они вовсе не содержат в себе ничего невозможного».

Однако никто не сумел отыскать экспериментальные подтверждения таких возможностей, и эта область науки заглохла. Учась в Кембридже, Эдвин Эбботт слышал отголоски сих тщетных усилий, о них время от времени упоминалось в научной литературе, но большинство физиков не принимало их всерьез. О тех математиках, которые все-таки продолжали рассматривать такие возможности, обычно говорили, что они зря тратят время. Даже Эйнштейн некогда присоединился к такому осмеянию. Еще в 1902 году он писал Милеве: «Гроссман затеял диссертацию на тему, которая связана со всякими плясками вокруг неевклидовой геометрии. Уж не знаю, что это такое». Но теперь, в 1912-м, взгляды Эйнштейна успели перемениться. «Я проникся глубоким уважением к математике!» – признавался он.

* * *

Давно забытые инструменты, которые математики-первопроходцы еще в XIX столетии разработали для изучения геометрии искривленных пространств, теперь могли принести ему неоценимую пользу. Они идеально подходили для той задачи, которую пытались решить Эйнштейн с Гроссманом. Это стало особенно очевидным, когда кто-то из них вспомнил, что математик Бернхард Риман, один из протеже Гаусса, на своей лекции 1854 года (которую посетил и престарелый Гаусс) продемонстрировал, как «существа, обитающие на [любой] поверхности, могут открыть кривизну своего мира и вычислить ее в любой точке». Эта идея, по сути, просто развивала наблюдения, уже сделанные картографами. Если треугольники «вспучиваются», это означает, что поверхность, на которой они существуют, подобна поверхности нашей сферической Земли. Если же треугольники «усыхают», сжимаясь внутрь, это означает, что речь идет о вогнутой поверхности – и все это можно увидеть, не выходя за пределы поверхности. Мистер А. Квадрат, обитающий в двухмерной вселенной, мог бы применить эти операции для того, чтобы выяснить, что он живет на плоской поверхности, еще до того, как зашедший к нему в гости Шар поднял его, чтобы Квадрат увидел свой мир сверху.

Эйнштейн осознал: если тщательно следовать процедурам Гаусса и Римана, мы тоже (измеряя углы на огромных расстояниях) сумеем выяснить, заставляет ли что-нибудь вспухать или сжиматься наше трехмерное пространство. Правда, без соответствующего измерительного оборудования этого не выявить: пространство перед нашими глазами кажется неискривленным. Человек лишен врожденной способности «видеть» более высокие измерения, будь он даже Эйнштейн. Однако при помощи особого рода расчетов мы все-таки можем узнать, есть ли в пространстве какая-то «кривизна», какие-то «кривые».