
|
||
|
|
||
|
|
Онлайн книга - Когнитивная психология | Автор книги - Роберт Солсо
Cтраница 152

Произвольное количество художников помечены как пчеловоды, есть также несколько пчеловодов, не являющихся художниками. Стрелками на схеме Джонсона-Лэрда и Стидмана показаны семантические связи классовой принадлежности. (В данном примере они обозначают отношение есть в высказывании: «Каждый художник есть пчеловод».) Вышеуказанную связь (Все А суть В) можно далее представить символически:
что опознается как посылка типа А.
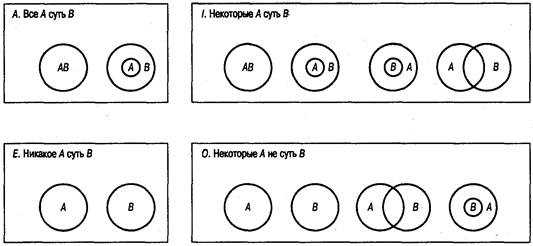
Рис. 14.2. Диаграммы, в которых представлены силлогизмы «все и некоторые А суть В» и «никакое или некоторые А суть В» Посылка типа I «Некоторые А суть В» (рис. 14.2) представляется так:
Посылка Е «Никакое А не суть Б»:
Посылка О «Некоторые А не суть В»:
Если вторая посылка имеет вид «Некоторые пчеловоды суть химики», то форма силлогизма будет следующей: Все художники суть пчеловоды. Некоторые пчеловоды суть химики. Или в символическом виде:
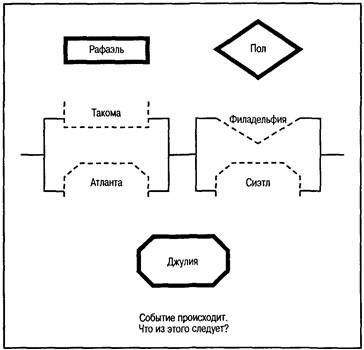
что часто приводит к неверному выводу: Некоторые из художников суть химики. Формулируя вывод, испытуемый старается проследить путь между конечными элементами в своей репрезентации частей силлогизма. Эта ситуация во многом напоминает решение задачи на мысленное картирование (например, определение кратчайшего пути в Бостон, Сан-Франциско, Атланту). Если есть хотя бы один положительный путь, то, вероятно, будет сделан неверный вывод; в силлогизме «художники-пчеловоды-химики» таким неверным выводом будет то, что некоторые художники суть химики. Изучение этого вопроса продолжили Клемент и Фэлман (Clement & Falmagne, 1986); они провели интересное исследование, в котором связывали логическое рассуждение со знанием о мире и мысленными образами. По существу, эти экспериментаторы варьировали степень образности терминов и «связность» условных утверждений в силлогизмах. Вы, вероятно, помните из нашего обсуждения в главе 10, что слова различаются по степени своей образности (например, образность слова «нищий» больше, чем у слова «контекст»). Связность показывает, насколько легко или естественно можно связать два действия. Примером использования в логическом силлогизме высокой образности может быть утверждение «Если этот человек хочет простой пончик, то...», а примером использования малой образности: «Если эта женщина реорганизует структуру компании, то...» Примеры утверждений с сильной и слабой связностью соответственно: «Если этот человек хочет простой пончик, то он идет в булочную через перекресток» и «Если этот человек выгуливает свою охотничью собаку, то укус насекомого расстроит его». Клемент и Фэлман использовали в силлогистических задачах все четыре возможные комбинации силлогистических утверждений (то есть большая образность — сильная связность, большая образность — слабая связность, малая образность — сильная связность и малая образность — слабая связность). Они обнаружили, что утверждения с большой образностью и сильной связностью обрабатывались значительно лучше, чем другие формы. Учитывая то, что мы знаем о сильном влиянии образности и связности на образование внутренних репрезентаций реальности, а также вышеописанную теоретическую модель Джонсона-Лэрда, этот вывод вполне логичен. Полезность диаграмм (например, диаграммы Венна) и образов при решении логических задач Бауэр и Джонсон-Лэрд (Bauer & Johnson-Laird, 1993) продемонстрировали с помощью сложных дедуктивных логических задач следующего вида: Рафаэль находится в Такоме, или Джулия находится в Атланте, или и то и другое. Джулия находится в Атланте, или Пол находится в Филадельфии, или и то и другое. Верное ли следующее заключение? Джулия находится в Атланте, или же Рафаэль находится в Такоме, а Пол -в Филадельфии. Если вы похожи на большинство испытуемых, принимавших участие в этом исследовании, вам трудно было обосновать это заключение. Теперь попробуйте визуализировать задачу с помощью диаграммы, приведенной на рис. 14.3.
Рис. 14.3. Диаграмма, представляющая задачу на двойную дизъюнкцию. Испытуемых попросили закончить путь слева направо, вставляя фигуры, соответствующие персонажам, в выемки. Так, Джулия могла быть в Атланте или Сиэтле, но не в обоих городах. Источник: Bauer & Johnson-Laird, 1993 Эта диаграмма — своего рода дорожная карта, по которой испытуемый должен путешествовать слева направо, вставляя фигуры (представляющие людей) во встречающиеся на пути выемки (представляющие города). Если путь не нарушен, путешествие может продолжаться. Так, если Джулия находится в Атланте, можно проехать через эту область. Джулия может быть в Атланте либо Сиэтле, или ее может не быть ни в одном из этих мест. В исследовании, проведенном в Принстонском университете (Bauer & Johnson-Laird, 1993), обнаружилось, что когда подобные задачи предъявлялись в форме диаграммы, студенты младших курсов решали их быстрее и делали больше верных заключений (приблизительно на 30% больше), чем когда задачи предъявлялись в вербальной форме. Из этого эксперимента мы можем сделать важный вывод — логически неподготовленные люди, а это большинство людей, склонны рассуждать, строя модели ситуации или рисуя диаграммы, ясно показывающие отношения. Например, когда вас просят решить классическую задачу по алгебре о дырявом ведре (имеющем три отверстия различных размеров, через которые вытекает вода, пока вы пытаетесь наполнить это ведро), разве вы не рисуете ведро, отверстия и наливной шланг? Я рисую. Исследования силлогизмов показывают, что в силлогистических задачах (а предположительно и в менее формальных видах логического мышления) люди делают выводы, сначала формируя внутренние репрезентации посылок — иногда вымышленные репрезентации. После того как внутренние репрезентации сформированы, к ним можно применить логическое мышление. Если репрезентация (или эвристика) нуждается в проверке (как в случае посылки «Все художники суть пчеловоды»), то для логической проверки вывода нужно попробовать разорвать пути между посылками и выводом.
|
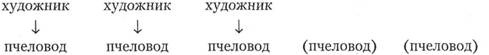

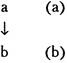
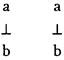
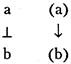

 Вернуться к просмотру книги
Вернуться к просмотру книги
 Перейти к Оглавлению
Перейти к Оглавлению
 Перейти к Примечанию
Перейти к Примечанию
 © 2020 LoveRead.ec - электронная библиотека в которой можно
© 2020 LoveRead.ec - электронная библиотека в которой можно