Укрощение бесконечности. История математики от первых чисел до теории хаоса - читать онлайн книгу. Автор: Йен Стюарт cтр.№ 78

В итоге в споре победил Сильвестр. Современные математики допускают существование явления, если оно логически непротиворечиво. Это может противоречить физическому опыту, что не имеет отношения к математической сущности. Тогда многомерные пространства ничуть не менее реальны, чем привычное нам пространство с тремя измерениями, поскольку мы можем без труда дать ему формальное определение.

Теперь математика многомерных пространств стала чисто алгебраической дисциплиной и основана на явных обобщениях, начинающихся с маломерных пространств. Например, любая точка на плоскости (в двумерном пространстве) может быть описана двумя координатами, а любая точка в трехмерном пространстве – тремя координатами. Отсюда остается сделать короткий шаг к описанию точки в четырехмерном пространстве как набору четырех координат и в более общем плане к определению точки в n-мерном пространстве как списку из n координат. Тогда само по себе n-мерное пространство (n-пространство) будет всего лишь набором таких точек.

Аналогичные алгебраические операции позволят вычислить расстояние между двумя любыми точками в n-пространстве, угол между двумя любыми линиями и т. д. Отныне и впредь главную роль играет воображение: самые обычные геометрические формы в двух или трех измерениях имеют прямые аналоги в n измерениях, и чтобы их найти, нужно описать знакомые формы с использованием алгебры координат, а затем расширить это описание до n координат.

Например, окружность на плоскости или сфера в трехмерном пространстве состоят из всех точек, что лежат на фиксированном расстоянии (радиус) от выбранной точки (центр). Явным аналогом для n-пространства будет всё множество точек, расположенных на фиксированном удалении от выбранной. Используя формулу для расстояний, мы превращаем это в чисто алгебраическое условие, и полученный в результате объект известен как (n − 1) – мерная гиперсфера, или (n − 1) – сфера. Число измерений уменьшается с n до n − 1, потому что, например, окружность в двумерном пространстве становится кривой, т. е. одномерным объектом. А сфера в пространстве является двумерной поверхностью. Сплошная гиперсфера в n измерениях называется n-шар. Таким образом, Земля – это 3-шар, а ее поверхность – 2-сфера.

В наше время такая точка зрения называется линейной алгеброй. Она используется не только в математике, но и в других областях науки, особенно в инженерии и статистике. Также она является стандартной техникой вычислений в экономике. Кейли утверждал, что его матрицы вряд ли получат какое-то практическое применение. Конечно, он ошибался.

К 1900-м гг. предсказание Сильвестра воплотилось в жизнь, особенно с освоением тех областей математики и физики, где концепция многомерного пространства стала серьезным подспорьем. Одной из таких областей стала теория относительности Эйнштейна – своего рода гениальный прорыв в четырехмерной геометрии пространства-времени. В 1908 г. Герман Минковский осознал, что три координаты обычного пространства, объединенные с еще одной, временной, как раз и образуют четырехмерное пространство-время. Всякая точка в нем называется событием: это некая частица, которая появилась на мгновенье, а потом исчезла. Теория относительности действительно имеет дело с физическими свойствами событий. В традиционной механике точечная частица, движущаяся в пространстве, имеет координаты (x(t), y(t), z(t)) в любой момент времени t, и это положение меняется со временем. С точки зрения пространства-времени Минковского собрание таких точек является кривой в пространстве-времени, мировой линией этой частицы, и это самостоятельный объект со своими свойствами, существующий всё время. В теории относительности четвертое измерение имеет единственную и неизменную интерпретацию – время.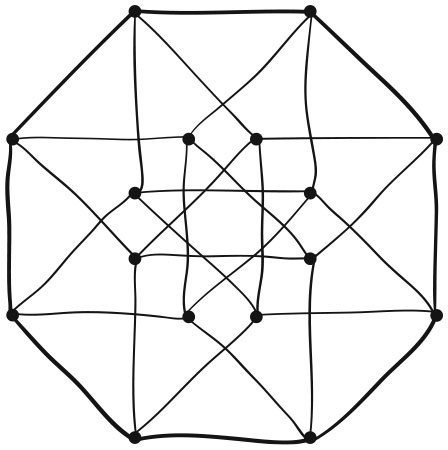

Четырехмерный гиперкуб, проекция на плоскость

Последующее включение силы притяжения в теории относительности потребовало широкого применения революционных римановских геометрий, хотя и модифицированных так, чтобы удовлетворять описанию Минковского для геометрии плоского пространства-времени. То, что происходит с пространством и временем в отсутствие массы, которая вызывает гравитационные искажения, Эйнштейн смоделировал как кривизну.

Математики предпочитали более гибкое понятие размерности и пространства, причем на рубеже XIX–XX вв. сама математика, судя по всему, всё больше требовала принятия многомерной геометрии. Теория функций двух комплексных переменных как естественное продолжение комплексного анализа нуждалась в представлении о пространстве с двумя комплексными измерениями. Но каждое такое измерение сводится к двум действительным измерениям, а значит, нравится вам это или нет, вы рассматриваете четырехмерное пространство. Римановское многообразие и алгебра многих переменных обеспечили дальнейшую мотивацию для исследований в этом направлении.

Однако еще одним мощным стимулом к принятию многомерной геометрии стало толкование механики в терминах обобщенных координат, сделанное Гамильтоном в 1835 г. Это исследование было инициировано Лагранжем в его «Аналитической механике» в 1788 г. Механическая система имеет столько же координат, сколько у нее степеней свободы – иными словами, возможностей изменять свое состояние. По сути, число степеней свободы – не что иное, как замаскированное измерение.

Например, необходимо шесть обобщенных координат, чтобы описать конфигурацию элементарного велосипеда: одна для угла, под которым руль крепится к раме, две для угловой позиции каждого из колес, еще одна для педальной оси и еще две для точек вращения педалей. Конечно, велосипед – трехмерный объект, но пространство для его возможных конфигураций получается шестимерным; и это одна из причин того, почему порой так трудно научиться ездить на велосипеде, пока вы не обретете сноровку. Вашему мозгу необходимо сконструировать внутреннее представление о взаимодействии этих шести переменных – научиться прокладывать курс в шестимерной геометрии велосипед-пространства. Когда велосипед на ходу, приходится следить, соответственно, за шестью скоростями: динамика, по существу, получится 12-мерной.

К 1920 г. это соперничество физиков, математиков и механиков благополучно разрешилось, и использование геометрического языка для задач со многими переменными – многомерной геометрии – уже не вызывало такого возмущения, разве что у некоторых философов. А к 1950 г. наука продвинулась вперед настолько, что для математиков стало совершенно естественным формулировать всё подряд в n измерениях с самого начала. Ограниченные теории о двух или трех измерениях оказались в списке устаревших и даже нелепых.

Язык многомерных пространств стремительно распространился во все области науки, захватив даже такие отрасли, как экономика и генетика. Сегодняшние вирусологи, например, воспринимают вирусы как точки в пространстве последовательности ДНК, у которых запросто может оказаться несколько сотен измерений. Под этим они подразумевают, что геном этих вирусов состоит из нескольких сотен оснований ДНК, и тогда геометрический образ вируса оказывается не просто отвлеченной метафорой: он становится эффективным способом решения проблемы.