
|
||
|
|
||
|
|
Онлайн книга - Укрощение бесконечности. История математики от первых чисел до теории хаоса | Автор книги - Йен Стюарт
Cтраница 74

Топология и реальный мир
Топологию изобрели, поскольку математика не могла функционировать без нее; это было вызвано решением ряда основных вопросов в областях вроде комплексного анализа. Она решает вопрос «Какова форма этого предмета?» в очень простом, но глубоком виде. Более привычные геометрические понятия, такие как длина, теперь можно было рассматривать как дополнительные свойства к основной информации, полученной с помощью топологии. Когда-то было высказано несколько первых топологических идей, но лишь к середине XIX в. топология стала полноправной областью математической науки со своими сущностью и влиянием, когда у математиков сложилось достаточно полное представление о топологии плоскостей, или двумерных форм. Расширение исследований на более многомерные пространства приняло бурный характер в конце XIX – начале XX в., во многом благодаря работам Анри Пуанкаре. Дальнейшие важные шаги были совершены в 1920-х гг. Новый взлет в этой области приходится на 1960-е, хотя по иронии судьбы именно тогда топология окончательно ушла от привычной нам прикладной науки. Разбив аргументы традиционных критиков чистой математики в ХХ в., развившаяся в результате теория стала неотъемлемой частью многих областей математической физики. Ученым удалось справиться даже с самой ее неразрешимой проблемой, а именно гипотезой Пуанкаре. Сейчас уже ясно, что главными препятствиями для развития топологии всегда становились ее внутренние противоречия, лучше всего решаемые с помощью абстрактных понятий. Ее связям с реальным миром пришлось подождать, пока не были до конца отработаны основные техники исследования. ЧТО ТОПОЛОГИЯ ДАЕТ НАМ В 1956 г. Джеймс Уотсон и Френсис Крик открыли тайну строения двойной спирали молекулы ДНК – основы, на которой записывается и хранится генетическая информация. Сегодня топология узлов используется для понимания того, как распутать две нити спирали, определяющих схему развития всякого живого организма. Спираль ДНК напоминает двужильную веревку, где одна жила виток за витком закручена вокруг другой. При делении генетическая информация попадает в обе новые клетки благодаря тому, что пряди спирали расплетаются и копируются, чтобы потом образовать пару. Любой, кому приходилось расплетать достаточно длинный обрезок обычной веревки, знает, как это трудно: нити норовят закрутиться в узлы в ответ на любую попытку их разделить. В случае ДНК всё еще хуже: сами спирали свернуты, как будто канат смотан в катушку. Представьте себе километровые нити, закрученные в подобие теннисного мяча, и вы получите отдаленное представление о сложной структуре ДНК в клетке. Генетической биохимии остается лишь искать способы сплетать и расплетать эти нити достаточно точно, аккуратно и быстро: на них держится сама жизнь! Но как этого добиться? Биологи научились с помощью ферментов разрезать цепочку ДНК на куски, достаточно короткие для подробных исследований. Любой сегмент ДНК представляет собой сложный молекулярный узел, причем один и тот же узел может стать неузнаваемым после неких манипуляций, искажающих его вид. Новые техники в изучении узлов открывают и новые направления атаки для молекулярных генетиков. И здесь топология узлов уже выходит за границы чистой математики, превращаясь в важный практический инструмент для биологов. Недавно была открыта математическая модель взаимосвязи между оборотами спирали ДНК и количеством образуемых ею суперклубков. 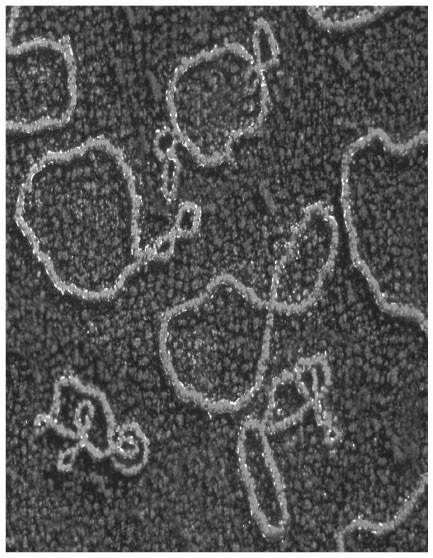
Узлы нитей ДНК Глава 16. Четвертое измерение
Геометрия за пределами нашего мира В своей научно-фантастической книге «Машина времени» Герберт Уэллс описывал скрытую природу пространства и времени в стиле, уже нам знакомом, но наверняка вызвавшем бы недоумение у современников из викторианской эпохи: «И всё же существуют четыре измерения, из которых три мы называем пространственными, а четвертое – временным». В поддержку своего мнения он добавляет: «Правда, существует тенденция противопоставить три первых измерения последнему, но только потому, что наше сознание от начала нашей жизни и до ее конца движется рывками лишь в одном направлении этого последнего измерения… Однако некоторый философские умы задавали себе вопрос: почему же могут существовать только три измерения? Почему не может существовать еще одно направление под прямым углом к трем остальным? Они пытались даже создать Геометрию Четырех Измерений». Его главный герой идет еще дальше: преодолевает традиционную ограниченность человеческого сознания и путешествует в четвертом измерении, времени, как если бы это было одно из «нормальных» измерений пространства. Четвертое измерение
Искусство автора научной фантастики состоит в умении подать читателям самые невероятные вещи, и Уэллс сообщает читателям, что всего около месяца тому назад профессор Саймон Ньюком излагал эту проблему перед Нью-Йоркским математическим обществом. Здесь Уэллс мог даже ссылаться на реальное событие. Нам известно, что Ньюком был маститым астрономом и даже читал лекцию о четырехмерном пространстве примерно в то же время. Он выражал свежие веяния в математической и научной мысли, освободившейся от традиционного представления о том, что пространство имеет только три измерения. Само по себе это не делает возможным путешествие во времени, но позволяет Уэллсу сформулировать некие наблюдения о человеческой натуре современников, отправив путешественника во времени в беспокойное будущее. «Машина времени», увидевшая свет в 1895 г., отражала одержимость четвертым измерением, свойственную викторианской эпохе. Это непостижимое, невидимое человеку пространство традиционно считалось местом обитания всяческих призраков, духов или даже самого Всевышнего. Четвертое измерение понравилось не только шарлатанам и писателям: о нем принялись рассуждать ученые, и понятие такого пространства формализовали математики. Прошло лишь несколько десятилетий, и мы видим, что математики привычно оперируют не только четырьмя, но и пятью, и шестью, и десятью, и миллионом, и даже бесконечным числом измерений. Приемы и образ мышления, сложившиеся в многомерной геометрии, стали применяться практически во всех отраслях науки – вплоть до биологии и экономики. Многомерные пространства пока остаются практически неизвестными вне научного сообщества, однако трудно представить себе современное мышление без использования этих методов, какими бы отстраненными они ни казались с точки зрения обыденной жизни. Ученые в попытке объединить две основные теории о законах существования физической вселенной, теорию относительности и квантовую механику, склоняются к предположению, что актуальное для нас пространство скорее имеет девять или десять измерений, а не три, как нам обычно кажется. В свете нового всплеска дискуссий о неевклидовой геометрии трехмерное пространство всё чаще рассматривается как всего лишь одно из многих, а не единственное возможное.
|
 Вернуться к просмотру книги
Вернуться к просмотру книги
 Перейти к Оглавлению
Перейти к Оглавлению
 Перейти к Примечанию
Перейти к Примечанию
 © 2020 LoveRead.ec - электронная библиотека в которой можно
© 2020 LoveRead.ec - электронная библиотека в которой можно