
|
||
|
|
||
|
|
Онлайн книга - Укрощение бесконечности. История математики от первых чисел до теории хаоса | Автор книги - Йен Стюарт
Cтраница 38

В 1677 г. он вывел правила дифференцирования суммы, произведения и частного для двух функций, а к 1680-му – формулу длины дуги кривой и объема тела вращения как интегралов от различных связанных величин. Нам известны все эти факты, а также относящиеся к ним даты из его неопубликованных записок, но впервые свои идеи о методах исчисления он опубликовал намного позже, в 1684 г. Якоб и Иоганн Бернулли сочли эти записи туманными, назвав их «скорее загадкой, чем объяснением». Но теперь понятно, что к тому моменту Лейбниц успел открыть значительную часть основ исчисления, с возможностью применить их для таких сложных кривых, как циклоида, и приблизиться к пониманию таких концепций, как кривизна. К несчастью, его записки слишком отрывочны и не поддаются прочтению. Ньютон
Еще одним создателем методов исчисления считается Ньютон. Двое его друзей, Исаак Барроу и Эдмунд Галлей, отдавали должное таланту ученого и убеждали в необходимости опубликовать его труды. Ньютон же очень плохо переносил критику и когда в 1672 г. издал свои исследования природы света, то услышал много нелестного о своей работе, что надолго отбило у него охоту предавать огласке свои открытия. Но эпизодически он всё же отваживался издать некоторые работы и даже написал две книги. А для себя Ньютон продолжал развивать свои идеи о тяготении, и в 1684 г. Галлей снова попытался уговорить его опубликовать эти труды. Но для этого, помимо страха перед критикой, существовало и техническое препятствие. В своих рассуждениях ученый был вынужден объявить планеты точечными частицами с массой, не равной 0, но нулевыми размерами, что не соответствовало действительности и заведомо привлекло бы к нему нежелательное внимание критиков. Он хотел бы заменить эти невероятные точки на сферические тела, но не мог доказать, что силы взаимного тяготения между сферами такие же, как и между предельно малыми точками с равной массой. Только в 1686 г. Ньютону удалось заполнить этот пробел, и в 1687 г. свет увидели «Математические начала натуральной философии». Они содержали множество свежих идей. Самыми важными стали математические формулы законов движения, расширяющие работы Галилея, и тяготения, основанные на законах Кеплера. Главный закон движения по Ньютону (есть и дочерние, следующие из него) утверждал, что сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорение. Иными словами, скорость является производной от положения тела, а ускорение – производная от скорости. Значит, даже для выражения закона Ньютона нам не обойтись без второй производной положения тела относительно времени, что в современном написании выглядит так: 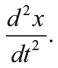
Только Ньютон вместо этого над x ставил две точки:
Закон тяготения утверждает, что все материальные частицы притягиваются друг к другу с силой, пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними. Так, сила тяготения между Землей и Луной станет сильнее в четыре раза, если Луна будет ближе к Земле в два раза, или в девять, если расстояние уменьшится втрое. И снова, поскольку речь идет о воздействии силы, здесь имеется вторая производная. Ньютон вывел свой закон из трех законов Кеплера о движении планет. Опубликованный им труд стал высшим достижением классической евклидовой геометрии. Ньютон сознательно избрал этот способ подачи материала, поскольку тот был основан на знакомых математических понятиях, а значит, менее уязвим для критиков. И всё же многие аспекты «Начал» появились на свет исключительно благодаря неопубликованным методам исчисления, открытым Ньютоном. Среди первых его работ в этой области есть статья под названием «Анализ с помощью уравнений с бесконечным числом членов», которую он распространил среди немногочисленных друзей в 1669 г. В современной терминологии он задается вопросом, как будет выглядеть уравнение для функции f(x), если площадь под графиком равна xm. (На самом деле вопрос касался более общих явлений, но давайте упростим.) К своему полному удовлетворению, он пришел к выводу, что ответ будет: f(x) = mxm − 1. ИСААК НЬЮТОН 1642–1727 
Ньютон рос на ферме в небольшой деревушке Вулсторп в графстве Линкольншир. Его отец скончался за два месяца до его рождения, и мать одна управлялась на ферме. Исаака отправили учиться в ближнюю школу, где он не выделялся особыми талантами, разве что отлично умел мастерить механические игрушки. Однажды он наполнил надувной шар горячим воздухом и испытал это средство воздухоплавания, посадив вместо пилота своего кота. Ни шар, ни кота никто больше не видел. Исаак поступил в Тринити-колледж в Кембриджском университете, где вполне успешно обучался по всем предметам – за исключением геометрии. Студентом он не производил впечатления будущего светила науки. Чума Позже, когда в 1665 г. великая эпидемия чумы опустошила Лондон и окрестности, студентов поспешно разослали по домам, пока мор не дошел до Кембриджа. Вернувшись на родительскую ферму, Ньютон стал серьезнее относиться к науке в целом и в частности к математике. Тяготение В 1665–1666 гг. он вывел свой закон тяготения, объясняющий движение планет, развил законы механики, чтобы проанализировать движения любого рода для всех физических тел, изобрел дифференциальное и интегральное исчисления, совершил важные открытия в оптике. Что характерно, он не спешил публиковать свои труды, но как ни в чем не бывало вернулся в колледж, получил степень магистра и стал членом Тринити-колледжа. Затем его избрали на должность Лукасовского профессора математики, а в 1669 г. подал в отставку предыдущий профессор, Барроу. Ньютон не прославился как преподаватель, на его лекциях было мало студентов. Подход Ньютона к вычислению производных в основном напоминает подход Лейбница, только вместо dx он использовал o, а значит, его метод грешил той же логической проблемой: он давал приблизительный результат. Однако Ньютону удалось показать: если принять о за бесконечно малую величину, приближение станет намного точнее. И когда мы дойдем до предела, где o станет такой малой, какой нам угодно, ошибка исчезнет. Поэтому Ньютон утверждал, что его результат точен. Он изобрел новое слово «флюксия», чтобы подчеркнуть главную идею: величина стремится к 0, но никогда не достигает его.
|
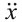 .
. Вернуться к просмотру книги
Вернуться к просмотру книги
 Перейти к Оглавлению
Перейти к Оглавлению
 Перейти к Примечанию
Перейти к Примечанию
 © 2020 LoveRead.ec - электронная библиотека в которой можно
© 2020 LoveRead.ec - электронная библиотека в которой можно