Укрощение бесконечности. История математики от первых чисел до теории хаоса - читать онлайн книгу. Автор: Йен Стюарт cтр.№ 11

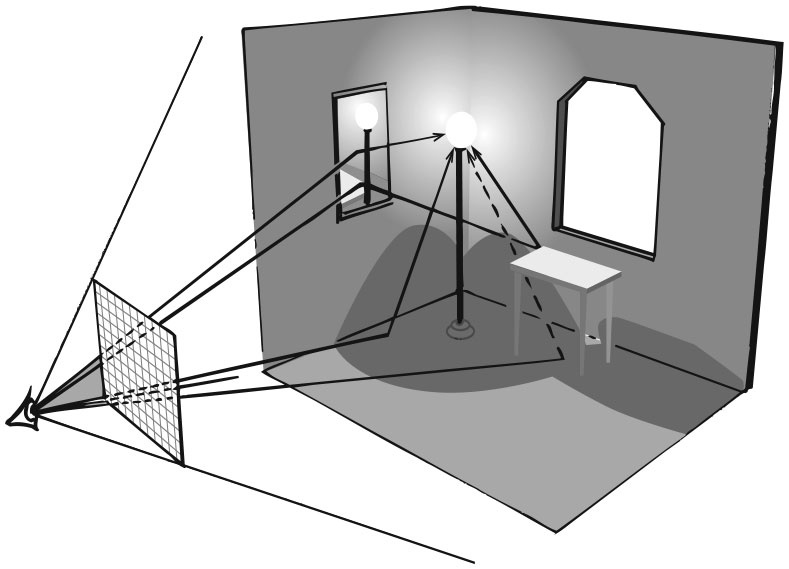
Принцип трассировки луча и получение отражения

Откуда взялись привычные нам цифры

На Западе многие знакомы по крайней мере с одной альтернативной системой – римскими цифрами. Например, год 2007 в ней выглядит как MMVII. Многие из нас смогут, если им напомнить, назвать по меньшей мере два способа изображения чисел, которые не являются целыми: обычные дроби, как ³/₄, и десятичные, например 0,75. Но есть еще один способ цифровой записи, используемый в калькуляторах: экспоненциальная запись для изображения сколь угодно больших и сколь угодно малых чисел, например 5 × 10⁹ для пяти миллиардов (часто в виде выражения 5Е9 на экране калькулятора) или 5 × 10^–6 для пяти миллионных.

Эти системы символов развивались тысячелетиями, и в культурах появлялись самые разные их альтернативы. Мы уже упоминали о шестидесятеричной системе вавилонян (которая, естественно, удовлетворила бы любое существо с 60 пальцами) и более простые, но ограниченные египетские символы со странным делением на доли. Позже в Центральной Америке майя изобрели и использовали двадцатеричную систему. Человечество остановилось на современной символике относительно недавно, и она также прошла через фильтр из традиций и условностей. И хотя математика – наука концепций, а не символов, удачный выбор символов для нее очень важен.

Историю символов для изображения цифр продолжили древние греки. Греческая геометрия стоит на порядок выше вавилонской, а вот арифметика – насколько мы можем судить по сохранившимся источникам – нет. Греки даже сделали большой шаг назад: они не воспользовались возможностями позиционной системы счисления. Они предпочли особые символы для чисел, кратных 10 или 100, так что, например, символ для 50 имел мало общего с изображениями 5 или 500.

Первые свидетельства записи чисел в Греции датируются примерно 1100 г. до н. э. Около 600 г. до н. э. они изменились и к 450 г. до н. э. скорректировались еще раз с принятием аттической системы счисления, немного похожей на римскую. В ней использовались символы I, II, III и IIII для чисел 1, 2, 3 и 4. Для числа 5 греки взяли заглавную «пи» (Π), возможно потому, что это первая буква в слове «пента» («пять»), 10 изображалось как Δ, первая буква в слове «дека» («десять»), 100 – как Η, первая буква в «гекатон» («сотня»), 1000 – как Ξ, первая буква «хилиои» («тысяча»), 10 000 – как Μ, первая буква «мюриой» («мириада».). Позже Π заменили на Γ. Итак, число 2178, например, было бы записано как ΞΞΗΔΔΔΔΔΔΔΓIII.

Пифагорейцы сделали числа основой своей философии, но мы так и не знаем, как они их изображали. Их одержимость квадратными и треугольными числами позволяет предположить, что они обозначали числа сочетаниями точек. В период классицизма, между 600 и 300 г. до н. э., греческая система снова изменилась, и 27 разных букв их алфавита стали выражать числа от 1 до 900, как в этой таблице.

Здесь мы уже видим строчные греческие буквы, дополненные тремя дополнительными, заимствованными из финикийского алфавита: 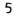(стигма), (коппа) и (сампи).