Вселенная Стивена Хокинга - читать онлайн книгу. Автор: Стивен Хокинг cтр.№ 27

Могли ли из неоднородностей, наличие которых требуется для объяснения существования звезд и галактик, образоваться в существенном количестве «первичные» черные дыры? Это, совершенно очевидно, зависит от конкретных особенностей ранней Вселенной. Поэтому если бы нам удалось установить количество первичных черных дыр в настоящее время, это позволило бы многое узнать о начальных стадиях эволюции космоса. Первичные черные дыры с массами более миллиарда тонн (масса крупной горы) регистрируются только по их гравитационному воздействию на другое, видимое, вещество или на расширение Вселенной. Но, как мы узнаем в следующей главе, черные дыры в действительности не совсем черные: они светятся, как раскаленные объекты, и чем они меньше, тем свечение сильнее. Потому – парадоксальным образом – может оказаться, что обнаружить мелкие черные дыры легче, чем крупные!

До 1970 года мои изыскания в области общей теории относительности касались в основном вопроса о том, существовала ли сингулярность в момент Большого взрыва. Но однажды вечерорм в ноябре того года, вскоре после рождения дочери Люси, я задумался о черных дырах, готовясь ко сну. Из-за моей болезни процесс это довольно медленный, поэтому у меня было много времени для размышлений. Тогда еще не существовало ясного представления о том, какие точки пространства-времени находятся внутри черной дыры, а какие – снаружи. Я уже обсуждал с Роджером Пенроузом идею определить черную дыру как множество событий, из которых невозможно уйти на большое расстояние, и это определение сейчас стало общепринятым. Оно означает, что граница черной дыры – горизонт событий – образована путями лучей света, которые и не сворачивают к сингулярности, и не могут покинуть черную дыру, оставаясь на грани между двумя «маршрутами» (рис. 7.1). Это напоминает попытку убежать от полицейских, когда преступник остается на шаг впереди, но при этом не в состоянии полностью избавиться от преследователей!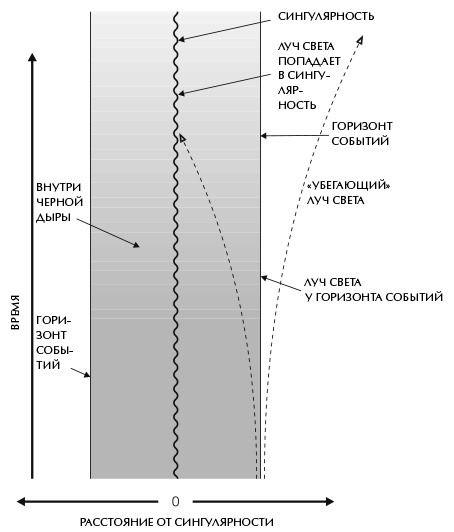

Рис. 7.1

Внезапно я понял, что пути этих лучей никогда не сблизятся друг с другом. Если бы это произошло, то рано или поздно они бы пересеклись. Это все равно что встретить другого беглеца, удирающего от полиции в противоположном направлении, – оба оказались бы в наручниках! (Или, в нашем случае, упали бы в черную дыру.) Но если бы черная дыра поглотила эти лучи, они не могли бы находиться на ее границе. Посему пути лучей на горизонте событий всегда должны быть параллельны друг другу или расходиться. Можно взглянуть на происходящее и с другого угла: горизонт событий, то есть границу черной дыры, можно сравнить с краем тени – тени неминуемой гибели. Если посмотреть на тень, которую отбрасывает предмет, освещенный удаленным источником, например Солнцем, то видно, что лучи света на краю тени не сближаются друг с другом.

Если пути лучей света, образующие горизонт событий – границу черной дыры, – никогда не сближаются, то площадь горизонта событий может оставаться неизменной или увеличиваться со временем, но ни в коем случае не уменьшаться. Ведь это означало бы, что как минимум часть лучей света на границе должны сближаться. В действительности площадь эта увеличивается каждый раз, когда вещество или излучение падают в черную дыру (рис. 7.2). А при столкновении или слиянии двух черных дыр и последующем образовании новой черной дыры площадь горизонта событий последней будет больше или равна сумме площадей горизонтов событий исходных черных дыр (рис. 7.3). Это свойство «неуменьшения» площади горизонта события накладывает важное ограничение на возможное поведение черных дыр. Я так разволновался из-за этого открытия, что той ночью почти не спал. На следующий день я позвонил Роджеру Пенроузу, и он согласился со мной. Вообще-то я думаю, что он уже знал об этом свойстве площади [горизонта событий]. Правда, он использовал немного иное определение черной дыры. Он не осознавал, что оба определения задают одни и те же границы черной дыры и, следовательно, одно и то же значение площади при условии, что черная дыра достигла состояния, которое не меняется со временем.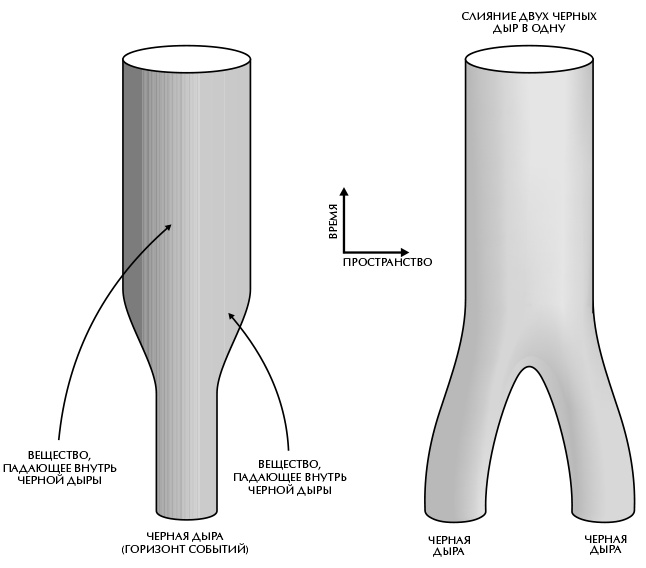

Рис. 7.2 и 7.3

«Неуменьшение» площади черной дыры отсылает нас к понятию энтропии – физической величине, которая является мерой хаоса в системе. С точки зрения здравого смысла, если никак не вмешиваться в ход событий, то степень беспорядка имеет свойство увеличиваться. (Чтобы убедиться в этом, достаточно просто перестать заниматься ремонтом в доме!) Из беспорядка можно получить порядок (например, покрасить стены), но это потребует усилий и энергии, а значит, уменьшит количество «упорядоченной» энергии в нашем распоряжении.

Точная формулировка этой идеи известна как второе начало термодинамики. Закон гласит, что энтропия изолированной системы всегда возрастает и что при объединении двух систем энтропия объединенной системы больше суммы энтропий исходных систем. Рассмотрим, например, систему молекул газа в контейнере. Молекулы можно представить как маленькие бильярдные шарики, которые постоянно сталкиваются друг с другом и отскакивают от стенок емкости. Чем выше температура газа, тем быстрее движутся молекулы, тем, следовательно, чаще и сильнее они сталкиваются со стенками и тем выше создаваемое ими давление на стенки. Предположим, что первоначально молекулы были сосредоточены в левой стороне контейнера, отделенной перегородкой. Если убрать перегородку, молекулы будут стремиться заполнить обе половины контейнера. В какой-то момент они все случайно могут оказаться в правой или левой части контейнера, но намного больше вероятность того, что количество молекул в правой и левой частях будет практически одним и тем же. Такое состояние менее упорядоченное – или более неупорядоченное, – чем исходное состояние, когда молекулы находились с одной стороны. Поэтому говорят, что энтропия газа возросла. Аналогичным образом можно представить себе систему из двух контейнеров, один из которых содержит молекулы кислорода, а другой – молекулы азота. Если соединить контейнеры и убрать разделяющую их стенку, то молекулы кислорода и азота начнут смешиваться. Наиболее вероятно, что вскоре оба контейнера будет заполнять практически однородная смесь молекул кислорода и азота. Это состояние менее упорядоченное и поэтому характеризуется бо́льшей энтропией, чем исходное состояние газов в двух отдельных контейнерах.

Второе начало термодинамики – в отличие, например, от ньютоновского закона гравитации и прочих физических законов – представляет особый случай: оно справедливо не всегда, а лишь в подавляющем большинстве случаев. Вероятность того, что все молекулы в первом контейнере некоторое время спустя окажутся в одной его половине, равна одному шансу из многих миллионов миллионов, но это все же может произойти. Однако появляется куда более простой способ нарушить второе начало термодинамики, когда под рукой имеется черная дыра: достаточно бросить туда некоторое количество вещества с большой энтропией, например контейнер с газом. В этом случае суммарная энтропия вещества вне черной дыры уменьшится. Конечно, можно сказать, что энтропия всего вещества, включая энтропию внутри черной дыры, и не подумает уменьшаться. Но ведь мы не можем заглянуть за горизонт событий и выяснить, какова энтропия заключенного за ним вещества. Было бы прекрасно, если бы у черной дыры был параметр, по которому внешний наблюдатель мог определить ее энтропию и который возрастал бы каждый раз, когда материя, несущая энтропию, падала в черную дыру.