
|
||
|
|
||
|
|
Онлайн книга - Увлекательно о космосе. Межпланетные путешествия | Автор книги - Яков Перельман
Cтраница 48

Продолжительность перелетов Перелет на Венеру. Продолжительность этого перелета, при условии минимальной затраты горючего, определится, если будет известен период обращения воображаемой планеты по эллипсу TV (рис. 60). Если S – Солнце, то ST = 150 × 106 км, SV = 108 × 106 км; среднее расстояние воображаемой планеты от Солнца равно ½ (150 + 108) × 106 = 129 × 106 км. По третьему закону Кеплера 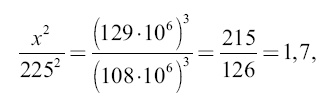
где x – продолжительность обращения воображаемой планеты, а 225 суток – продолжительность обращения Венеры; х = 225√1,7 = 293 сут. Значит, полет в один конец займет 147 суток. Перелет на Марс. Время перелета определяется из пропорции: 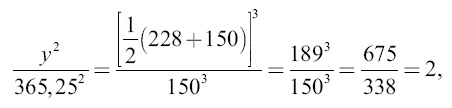
откуда у = 519 сут. Значит, перелет в один конец продлится 259 суток. 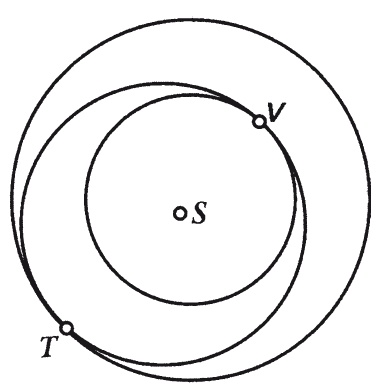
Рис. 60. Маршрут перелета с Земли (Т) на Венеру (V) 5. Внеземная станция
Для относящихся сюда расчетов воспользуемся рис. 54. Круг радиуса г пусть изображает земной шар, а эллипс – тот путь, по которому звездолет из точки А земной поверхности (экватора) долетает до круговой орбиты искусственного спутника. Прежде всего вычислим, каков должен быть радиус круговой орбиты (не изображенной на чертеже) этого спутника, чтобы время его обращения равнялось земным суткам. Применим третий закон Кеплера, зная, что Луна обходит Землю в 27,3 суток на расстоянии 60,3 земного радиуса от центра Земли: 
откуда 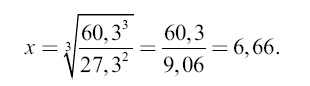
Итак, внеземная станция должна находиться в расстоянии 6,66 земного радиуса от центра Земли, чтобы период обращения равнялся 24 ч. Скорость, которую нужно сообщить на Земле звездолету, чтобы он достиг орбиты такого искусственного спутника, есть скорость в точке А эллипса (рис. 59). Вычислим ее по формуле (8): 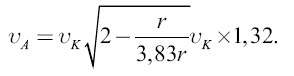
Здесь υК — скорость свободного кругового обращения небесного тела около центра Земли на расстоянии 1 земного радиуса, то есть 7,92 км/с. Следовательно, искомая скорость υА отлета υа = 7,92 × 1,32 = 10,5 км/с [48]. С какой скоростью звездолет достигнет орбиты искусственного спутника? Другими словами, какова скорость в точке В эллипса, противолежащей точке А? Находим ее, пользуясь вторым законом Кеплера: так как площади, описываемые радиусами-векторами в 1 с, равны, то 10,5 × г =x × 6,66 г, откуда 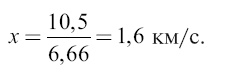
Сравним ее со скоростью движения внеземной станции по своей круговой орбите; последняя скорость, очевидно, в 6,66 раза больше скорости движения точек земного экватора (0,465 км): 0,465 × 6,66 = 3,1 км/с. Значит, звездолету понадобится еще дополнительная скорость в 3,1–1,6 = 1,5 км/с, чтобы пристать к внеземной станции. Далее, скорость, с какой звездолет должен покинуть внеземную станцию для достижения, например, орбиты Луны, вычислим по формуле (8), вообразив соответствующий эллипс, охватывающий орбиту станции и касающийся изнутри орбиты Луны: 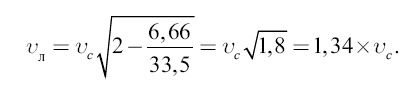
Так как скорость станции (υс) равна 3,1 км/с, то искомая скорость равна 1,34 × 3,1 = 4,1 км/с. Это всего на 300 м меньше той скорости, какая нужна здесь для полного освобождения от земного притяжения (3,1 × √2 = 4,4 км|. Если принять во внимание, что сама станция-спутник обладает скоростью в том же направлении, то для достижения Луны с внеземной станции понадобится лишь дополнительная скорость в 4,1–3,1 = 1 км/с. Соответствующее отношение
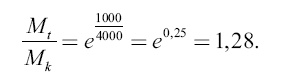
Масса горючего должна составлять менее – ½ массы ракеты после взрывания. Даже если мы желаем, чтобы звездолет мог возвратиться на внеземную станцию, то есть чтобы он сохранил запас горючего, достаточный для торможения (0,28 окончательной массы), мы должны снабдить его первоначально запасом горючего, составляющим только 0,4 веса всей заряженной ракеты. Отсюда очевидна огромная выгода создания внеземной станции в смысле облегчения остальных задач звездоплавания. 6. Давление внутри пушечного снаряда
Нам придется пользоваться лишь двумя формулами равноускоренного движения, именно: 1. Скорость υ в конце t-й секунды равна at, где а – ускорение: υ = at. 2. Пространство S, пройденное в течение t секунд, определяется формулой: 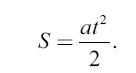
|
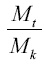 масс заряженной и незаряженной ракет при скорости вытекания газа 4000 м равно
масс заряженной и незаряженной ракет при скорости вытекания газа 4000 м равно Вернуться к просмотру книги
Вернуться к просмотру книги
 Перейти к Оглавлению
Перейти к Оглавлению
 Перейти к Примечанию
Перейти к Примечанию
 © 2020 LoveRead.ec - электронная библиотека в которой можно
© 2020 LoveRead.ec - электронная библиотека в которой можно