Психология развития. Методы исследования - читать онлайн книгу. Автор: Скотт Миллер cтр.№ 63

И последнее замечание — статистическая значимость не гарантирует того, что результаты имеют некоторую научную ценность. «Значимость» в том смысле, в котором этот термин употребляется здесь, имеет отношение только к статистической вероятности, а не к теоретической или практической важности. Различие между полами в уровне агрессии может быть истинным, в том смысле, что оно не случайно и не обусловлено неудовлетворительной валидностью. Достаточно ли велико это различие, чтобы что-то значить — в отношении, например, того, как воспитатели должны вести себя с мальчиками и девочками, — отдельный вопрос. Важно помнить, что статистическая значимость различия зависит не только от величины разницы, но и от объема выборки. В достаточно большой выборке даже незначительное различие достигает уровня значимости. Мы еще вернемся к этому вопросу, когда будем рассматривать величину эффекта.

Для многих студентов слово «статистика» ассоциируется с зазубриванием формул и бесконечными часами утомительных подсчетов. В действительности профессиональный исследователь если и может воспроизвести, то не более нескольких формул и тратит на расчеты совсем немного времени. В этом нет необходимости: формулы есть в учебниках или заложены в компьютер, а расчеты можно производить на калькуляторе, на компьютере (или предоставить это студенту-лаборанту!). Что значительно важнее, это знать, какого рода статистический анализ подходит и информативен для определенного рода данных. При выборе наиболее подходящего статистического показателя учитывается множество факторов. В этом разделе мы рассмотрим три из них: уровень, па котором измеряется зависимая переменная, распределение значений зависимой переменной и план исследования.

Понятие уровня, или шкалы измерения было введено в главе 4. Вспомним, что выделяют четыре уровня измерения: поминальный, или качественное обозначение результатов; порядковый, или ранжирование результатов по некой шкале количественных значений; интервальный, или распределение результатов по шкале количественных значений, которые не только упорядочены, но и равноудалены друг от друга; и уровень отношений, или равномерное упорядочение результатов по шкале количественных значений, имеющей абсолютный нуль.

Уровень измерения является одним из факторов, определяющих, какой из статистических критериев уместнее всего употребить. Некоторые критерии, включая и t, используются только тогда, когда измерение производится на шкале интервалов или шкале отношений. Основание для этого требования станет очевидным при анализе формулы на рис. 7.1. Для расчета f-критерия мы должны произвести ряд арифметических операций с числами — сложить, а затем разделить, чтобы получить среднее, вычесть каждое число из среднего, чтобы' получить показатель отклонения и т. д. Эти операции имеют смысл только в том случае, если числа, с которыми мы работаем, являются точным отображением количественного значения, а не просто названиями или порядковыми номерами. Показатели частоты из табл. 7.1 отвечают указанному требованию, и, следовательно, к этим данным f-критерий применим. Однако f-критерий не подошел бы, если бы наши данные были основаны на описанной ранее рейтинговой шкале. Мы могли бы, к примеру, сложить рейтинговую оценку 5 («крайне агрессивный») с рейтинговой оценкой 1 («совершенно неагрессивный») и получили бы среднее 3 («умеренно агрессивный»). (Вскоре я уточню это замечание. Кроме того, необходимо помнить, что не все специалисты в области теории измерения и статистики сходятся во мнении по вопросу связи между шкалами измерения и статистическими показателями, — см. Cliff, 1993; Michell, 1986.)

Использование некоторых статистических критериев связано с определенными предположениями о распределении оцениваемых этим критерием показателей. В частности, так называемые параметрические критерии зависят от определенных

предположений о распределении данных. Это, фактически, и является смыслом термина «параметрический»: статистический анализ зависит от валидности некоторых предположений в отношении «параметров» популяции, к которой принадлежит выборка. Рассмотренный выше t-критерий — пример параметрического критерия; критерий, используемый в дисперсионном анализе (ANOVA), которому посвящен следующий раздел, — еще один пример.

Если говорить более конкретно, в основе использования большинства параметрических критериев лежит два допущения. Первое состоит в том, что показатели распределены по закону нормального распределения. Второе — что дисперсия в сравниваемых группах одинакова. Второе допущение распространяется не на все случаи, но применимо ко многим, часто используемым параметрическим критериям, включая -критерий и F-критерий дисперсионного анализа.

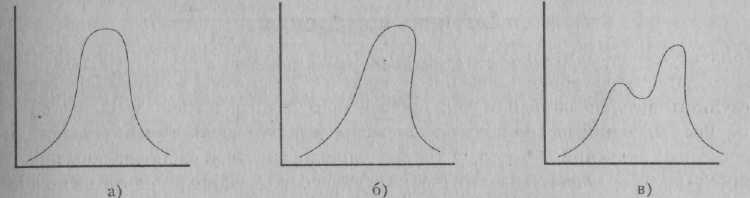
Рис. 7.1. Примеры нормального и ненормального распределения

Мы уже обсуждали понятие дисперсии. Рассмотрим теперь необходимые условия нормального распределения. На рис. 7.1 (а) изображено нормальное распределение. Термин «нормальное распределение* используется в отношении классической колоколообразной кривой, к распределению, в котором среднее, медиана и мода совпадают, а показатели постепенно уменьшаются по мере удаления от этого центра. Рис. 7.1 (б) и (в), напротив, иллюстрируют распределение, явно отличное от нормального.

Между уровнем измерения и распределением есть определенная связь. Показатели номинальных и порядковых шкал не могут иметь нормальное распределение. Что касается номинальной шкалы, в ней нет количественных значений, и поэтому вопрос распределения по шкале количественных значений не стоит; все, что здесь возможно, это подсчет частоты случаев в каждой из категорий. Если говорить о порядковой шкале, то нам неизвестна разница между показателями, а следовательно, и их распределение. Кроме того, в абсолютно упорядоченной шкале (то есть при отсутствии совпадений) на каждый уровень шкалы приходится всего по одному случаю; поэтому теоретически распределение будет плоским. Таким образом, необходимым условием нормального распределения является наличие шкалы отношений или интервалов. Тем не менее это недостаточное условие, поскольку кривая показателей все еще может выглядеть так, как на рис. 7.1 (б) или (в). Однако по закону нормального распределения могут быть распределены только показатели, соответствующие определенным шкалам.

Мы только что рассмотрели предположения, лежащие в основе использования параметрических критериев t и F. Скажем теперь несколько слов об альтернативе

Логика проверки с использованием критерия хи-кнадрат: определение того, насколько полученные

значения частоты в каждой клетке таблицы отклоняются от ожидаемой частоты, если допустить

отсутствие различий между группами.