
|
||
|
|
||
|
|
Онлайн книга - Битва при черной дыре. Мое сражение со Стивеном Хокингом за мир, безопасный для квантовой механики | Автор книги - Леонард Сасскинд
Cтраница 6

Может ли снаряд [17] — камень, пуля или хотя бы элементарная частица — вырваться из гравитационного притяжения Земли? С одной стороны — да, с другой — нет. Гравитационное поле массы нигде не заканчивается; оно тянется бесконечно, становясь все слабее и слабее по мере увеличения расстояния. Так что брошенный вверх снаряд никогда полностью не избавится от земного притяжения. Но если снаряд брошен вверх с достаточно большой скоростью, он будет удаляться вечно, поскольку убывающая гравитация слишком слаба, чтобы развернуть его и притянуть назад к поверхности. В этом смысле снаряд может вырваться из земного тяготения. Даже самый сильный человек не имеет шансов выбросить камень в открытый космос. Высота броска профессионального бейсбольного питчера может достигать 70 метров, это около четверти высоты Эмпайр-стейт-билдинг. Вели пренебречь сопротивлением воздуха, пуля, выпущенная из пистолета, могла бы достичь высоты 5 километров. Но существует особая скорость — называемая скоростью убегания [18], — которой едва хватает, чтобы вывести объект на вечно удаляющуюся траекторию. Начав движение с любой меньшей скоростью, снаряд упадет обратно на Землю. Стартовав с большей скоростью, он уйдет на бесконечность. Скорость убегания для поверхности Земли составляет 40 000 км/ч (11,2 км/с) [19]. Давайте временно станем называть звездой любое массивное небесное тело, будь то планета, астероид или настоящая звезда. Земля — это просто маленькая звезда, Луна — еще меньшая звезда и т. д. По ньютоновскому закону тяготения, гравитационное воздействие звезды пропорционально ее массе, так что совершенно естественно, что и скорость убегания тоже зависит от массы звезды. Но масса — это только полдела. Другая половина — это радиус звезды. Представьте себе, что вы стоите на земной поверхности и в это время некая сила начинает сжимать Землю, уменьшая ее размеры, но без потери массы. Если вы остаетесь на поверхности, то сжатие будет приближать вас ко всем без исключения атомам Земли. При сближении с массой воздействие ее гравитации усиливается. Ваш вес — функция гравитации — будет возрастать, и, как нетрудно догадаться, преодолевать земное тяготение будет все трущее. Этот пример иллюстрирует фундаментальную физическую закономерность: сжатие звезды (без потери массы) увеличивает скорость убегания. Теперь представьте себе прямо противоположную ситуацию. По каким-то причинам Земля расширяется, так что вы удаляетесь от массы. Тяготение на поверхности будет становиться слабее, а значит, из него легче вырваться. Вопрос, поставленный Митчелом и Лапласом, состоял в том, может ли звезда иметь такую большую массу и столь малый размер, чтобы скорость убегания превзошла скорость света. Когда Митчел и Лаплас впервые высказали эти пророческие мысли, скорость света (обозначаемая буквой с) была известна уже более ста лет. Датский астроном Оле Рёмер в 1676 году определил, что она составляет колоссальную величину — 300 000 км (это примерно семь оборотов вокруг Земли) за одну секунду: с = 300 000 км/с При такой колоссальной скорости, чтобы удержать свет, требуется чрезвычайно большая или чрезвычайно сконцентрированная масса, однако нет видимых причин, по которым такой не могло бы существовать. В докладе Митчела Королевскому обществу впервые упоминаются объекты, которые Джон Уилер впоследствии назовет черными дырами. Вас может удивить, что среди всех сил гравитация считается чрезвычайно слабой. Хотя тучный лифтер и прыгун в высоту могут чувствовать себя по-разному, есть простой эксперимент, демонстрирующий, как слаба в действительности гравитация. Начнем с небольшого веса: пусть это будет маленький шарик пенопласта. Тем или иным способом придадим ему статический электрический заряд. (Можно просто потереть его о свитер.) Теперь подвесим его к потолку на нитке. Когда он перестанет крутиться, нить будет висеть вертикально. Теперь поднесите к висящему шарику другой подобный заряженный предмет. Электростатическая сила будет отталкивать подвешенный груз, заставляя нить наклоняться. 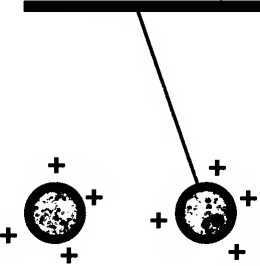
Того же эффекта можно добиться с помощью магнита, если висящий груз сделан из железа. 
Теперь уберите электрический заряд или магнит и попытайтесь отклонить подвешенный груз, поднося к нему очень тяжелые предметы. Их гравитация будет притягивать груз, но воздействие окажется столь слабым, что его невозможно заметить. Гравитация чрезвычайно слаба по сравнению с электрическими и магнитными силами. 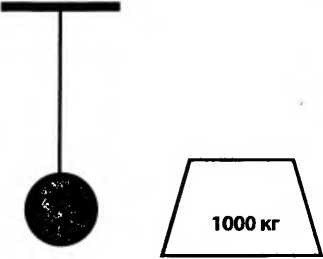
Но если гравитация так слаба, почему нельзя допрыгнуть до Луны? Дело в том, что огромная масса Земли, 6x1024 кг, с легкостью компенсирует слабость гравитации. Но даже при такой массе скорость убегания с поверхности Земли составляет меньше одной десятитысячной от скорости света. Чтобы скорость убегания стала больше с, придуманная Митчелом и Лапласом темная звезда должна быть потрясающе массивной и потрясающе плотной. Чтобы прочувствовать масштаб величин, давайте рассмотрим скорости убегания для разных небесных тел. Для покидания поверхности Земли нужна начальная скорость около 11 км/ с, что, как уже отмечалось, составляет примерно 40 000 км/ч. По земным меркам это очень быстро, но в сравнении со скоростью света подобно движению улитки. На астероиде у вас было бы куда больше шансов покинуть поверхность, чем на Земле. У астероида радиусом 1,5 км скорость убегания составляет около 2 м/с: достаточно просто прыгнуть. С другой стороны, Солнце много больше Земли, как по размеру, так и по массе [20]. Эти два фактора действуют в противоположных направлениях. Большая масса затрудняет покидание поверхности Солнца, а большой радиус, наоборот, упрощает. Масса, однако, побеждает, и скорость убегания для солнечной поверхности примерно в пятьдесят раз больше, чем для земной. Но она все равно остается много ниже скорости света.
|
 Вернуться к просмотру книги
Вернуться к просмотру книги
 Перейти к Оглавлению
Перейти к Оглавлению
 Перейти к Примечанию
Перейти к Примечанию
 © 2020 LoveRead.ec - электронная библиотека в которой можно
© 2020 LoveRead.ec - электронная библиотека в которой можно