Гейзенберг. Принцип неопределенности - читать онлайн книгу. Автор: Жозе Наварро Фаус cтр.№ 19

Вы уже знаете, что отправной точкой при создании матричной механики было представление об электроне как о частице, отправной точкой волновой механики – представление об электроне как о волне. Обе модели непротиворечивы и эквивалентны с математической точки зрения, однако это не помогало определить, что же такое электрон – частица или волна. Бор настаивал на том, что эти взаимоисключающие модели могут существовать одновременно, и считал, что они необходимы для полного описания физических явлений на атомном уровне. Продолжительные дискуссии совершенно вымотали и Бора, и Гейзенберга, и в конце февраля Бор отправился в отпуск в Норвегию. Вскоре после этого Гейзенберг открыл свои знаменитые неравенства.

В марте 1927 года ученый пишет в Копенгагене еще одну, крайне важную статью «О наглядном содержании квантовотеоретической кинематики и механики», где приводит соотношения, описывающие принцип неопределенности. Основная идея статьи приводилась в ее начале:

«Если мы хотим себе уяснить, что следует понимать под словом «положение объекта», например электрона (по отношению к заданной системе отсчета), необходимо указать определенные эксперименты, при помощи которых намереваются определить «положение электрона»; в противном случае это слово не имеет смысла».

Гейзенберг писал, что смысл физической теории заключен не в математических уравнениях, а в новых понятиях и их значении. До начала XX века основу физики составляла классическая механика Ньютона. В теории относительности были переопределены понятия пространства, времени и массы и продемонстрированы их ограничения при скоростях, сравнимых со скоростью света. Согласно Гейзенбергу, похожие изменения происходят и в том случае, если рассматривать объекты малой массы, которые перемещаются на очень малые расстояния, в частности электроны атомов.

Неопределенность и классические волны

На рисунке 1 показана волна, описываемая уравнением вида cos (2πk₀(х–х₀)), волновое число равно k₀. Следовательно, ее неопределенность равна Δk = 0. Волна определена на всем пространстве, поэтому можно сказать, что она имеет бесконечную пространственную неопределенность Δх = oo.

На среднем рисунке изображена суперпозиция пяти волн, волновое число которых, k, очень близко к k₀ . Эти волны изображены серым цветом, результирующая волна – черным. Из-за интерференции эта волна выглядит не так, как волна, изображенная вверху: в одних точках ее амплитуда увеличивается, в других – уменьшается. Рассмотрим суперпозицию бесконечного числа волн и присвоим каждой из них определенный вес, задаваемый гауссовой функцией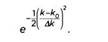

Иными словами, волновое число будет близко к k₀ с отклонением Δk. График гауссовой функции представлен на рисунке 2. Функция принимает максимальное значение тогда, когда волновое число совпадает с центральным значением. Мы описали отклонение графика функции, когда она принимает значение е^-1/2 , то есть примерно 0,61. На практике за пределами интервала, границы которого отстоят от центрального значения на три стандартных отклонения, значениями этой функции можно пренебречь. Результатом суперпозиции будет волна, подобная изображенной на рисунке 1, с волновым числом k₀. Она будет описываться функцией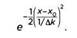

Эта совокупность волн называется гауссовым волновым пакетом, который, как вы увидели, распространяется не во всей области пространства, а лишь в окрестностях точки x₀ с отклонением Δх = 1/Δk. Иными словами, отклонения волновых чисел и размеры в пространстве связаны между собой: Δk • Δx = 1. Именно так выглядит соотношение Гейзенберга для классических волн.

Сделаем еще один шаг вперед и напомним, что импульс частицы определяется на основе соответствующего волнового числа: p = 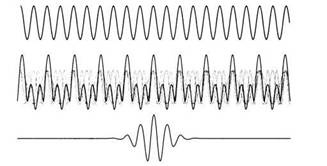hk. Редуцированная постоянная Планка указывает, что речь идет о квантовой механике. Результирующее соотношение будет записываться так: Δр • Δх = h, что соответствует неравенству Гейзенберга.

Рис. 1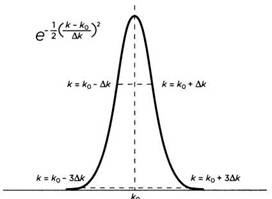

Рис. 2

Проблема заключается в том, что наблюдать это движение нельзя – мы можем увидеть лишь общее поведение большого числа атомов, проявлением которого служит, к примеру, частота света, излучаемого или поглощаемого ими. Для объяснения этих свойств требовалась новая механика, в которой были описаны «разрывы», проявлявшиеся в виде дискретных квантов, или «порций», энергии и кванто-вых скачков между энергетическими уровнями. Так как эти разрывы очень малы, их нельзя увидеть на макроуровне, и мир кажется нам непрерывным. Сам Гейзенберг говорил:

«Если допустить, что дискретность является в некотором роде типичной особенностью процессов, проходящих на малых расстояниях и в малые промежутки времени, то весьма вероятно, что мы придем к противоречию, говоря о понятиях «положение» и «скорость». Классическое представление о траектории частицы как о непрерывной кривой следует заменить дискретной последовательностью точек в пространстве и времени. В силу этого классические идеи нельзя использовать при одновременном измерении положения и импульса частицы».

Классическая частица описывается уравнениями, задающими ее положение и скорость в любой момент. Однако эти понятия имеют смысл для атомных частиц только в том случае, если мы говорим об их измерении. Иными словами, физик знает только то, что может измерить, – в этом и заключается принцип неопределенности.

Некоторые расчеты привели Гейзенберга к следующему результату. Допустим, что в эксперименте мы определили положение частицы x с точностью Δx, а также импульс частицы p с точностью Δp. Это означает, что положение частицы с некоторой вероятностью заключено на интервале между x – Δx и x + Δx. Может ли точность быть сколь угодно малой? Гейзенберг доказал, что это невозможно, так как произведение этих величин сопоставимо с постоянной Планка. Это соотношение записывается так: Δx • Δp ~ h. Это выражение передает взаимное ограничение: чем меньше будет один множитель, тем больше будет другой, чем точнее мы определим одну из этих величин, тем меньше будет точность измерения другой. Было строго доказано, что это соотношение имеет вид неравенства:

Δx – Δp=>h/2.

Произведение величин, показывающих, с какой точностью можно измерить положение частицы и ее импульс, ограничено редуцированной постоянной Планка h = h/(2π), разделенной на 2.