
|
||
|
|
||
|
|
Онлайн книга - Неизвестный алмаз. "Артефакты" технологии | Автор книги - Владимир Карасев
Cтраница 19

Нескрываемое удивление у нас вызвало состояние «обработанной» поверхности октаэдрической грани. Следует заметить, что эта грань является «твердой» гранью (111) в алмазе типа октаэдра (рис. 7.3). 
Рис. 7.3. Состояние поверхности алмазной грани после эксперимента Подобные «барханы» на поверхности алмаза могут образоваться только в одном случае – в случае нахождения поверхности алмаза в состоянии, близком к жидкому. А их линейные размеры никоим образом не связаны с размерностью зерна используемого абразива (-10/7 мкм). Геометрический размер «обработанной» грани -3 х 3 мм. Фото сделано в отраженном свете. 
Рис. 7.4. Отверстие в виде колодца в алмазе Характер расположения этих «барханов» при применении двухосевой системы обработки позволяет сделать предположение, что они образовались на плоскости октаэдра в мягком направлении (а) в последний момент отрыва инструмента от поверхности воздействия. Температура алмаза в процессе эксперимента при этом составляла ~23,5 °C. Но наибольшее удивление у нас вызвало возникшее на соседней грани шестигранное отверстие в виде колодца (отмечено стрелкой) (рис. 7.4). Входной диаметр этого углубления составил ~0,5 мм, а глубина ~ 0,7 мм. Структура стенок и дна этого «колодца» представляла собой многогранные рельефные образования и не носила следов ни химического воздействия атмосферы, ни какого-либо другого воздействия, отражающегося на их внутреннем состоянии (травления или полирования). И в заключение: как можно догадаться, под формулировкой «технологический алгоритм процесса обработки» скрываются определенные взаимодействия и программируемые величины приведенных выше параметров. Какие-то параметры у нас во многих случаях являются постоянными, какие-то приходится рассчитывать для конкретно поставленной задачи, а какие-то меняются в процессе воздействия. В этом случае постоянных накатанных приемов нет. Каждый раз к алмазу мы подходим избирательно, ибо каждый алмаз уникален. Результаты воздействия квантово-волнового метода на кристаллы алмаза показывают, что это действительно новый взгляд на процесс обработки алмаза. Получая многообразие экспериментальных данных, мы пока не можем в полной мере свести все результаты в какое-то обобщенное и завершенное понимание процесса. На сегодняшний день мы не вполне уверены в прогнозах, какое именно новое изделие (или прибор) может быть изготовлено из кристаллов природного алмаза с привлечением нашего метода. С одной стороны, нет видимых ограничений в его возможностях, с другой – нет полностью сформировавшегося взгляда о конкретном виде продукции, в которой все эти совокупные возможности могут быть реализованы в полной мере. Глава 8
Гипотезы квантово-волновой обработки Прежде чем попытаться обобщить полученные результаты проведенных экспериментов, обратимся еще раз к более подробному рассмотрению метода двухосевого воздействия инструмента на алмаз на конкретном примере. Обрабатывающий инструмент имеет ось вращения α (рис. 8.1). Эта подвижная ось перемещается вокруг неподвижной оси ß по траектории окружности с радиусом (ra). Величина (ra) является аппаратурным фактором и не меняется в процессе воздействия. Ось вращения а является центром инерции обрабатывающего инструмента, диаметр рабочей поверхности которого выбирается в зависимости от поставленной задачи воздействия и имеет размер в несколько раз больше, чем (ra). В данном случае в этой схеме плоскость чертежа можно условно рассматривать как 1/2 часть поверхности инструмента. Вполне очевидно, что вся рабочая поверхность инструмента одновременно перемещается вокруг неподвижной оси ß по траектории окружности с радиусом (ra), В этом случае любая точка касания инструмента с обрабатываемой поверхностью алмаза описывает аналогичную траекторию окружности по поверхности инструмента (окружность диаметром 2ra, рис. 8.1). 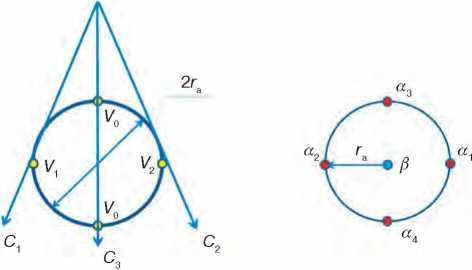
Рис. 8.1. Схема волнового воздействия В качестве примера циклического воздействия инструмента на кристалл алмаза рассмотрим эксперимент «мягкое направление» (см. рис. 7.2). Начальная (задаваемая) кристаллографическая ориентация обрабатываемой поверхности плоскости октаэдра (с учетом направления движения зерен абразива инструмента) была проведена относительно траекторий движения абразива по мягкому направлению а на рис. 7.2. Это направление соответствует движению зерен абразива С3 на рис. 8.1. Положение оси α в этом случае соответствует, например, положению α3 относительно оси ß. При этом линейная скорость движения зерен абразива составляет V0 и происходит эффективное воздействие инструмента по мягкому направлению а обрабатываемой поверхности. При эксцентричном перемещении оси α в положение α2, обрабатывающая поверхность инструмента также перемещается по окружности относительно неподвижной обрабатываемой плоскости октаэдра алмаза. Кристаллографическая ориентация траекторий движения зерен абразива относительно неподвижной плоскости октаэдра изменяется на С2, и совпадает с твердым направлением b2, поверхности октаэдра на рис. 7.2. Величина линейной скорости V2 при этом уменьшается относительно V0, поскольку уменьшается радиус движения зерен абразива инструмента на величину гa. При перемещении оси α в положение α4 инструмент относительно неподвижную обрабатываемой поверхности алмаза занимает позицию, аналогичной движению зерен абразива позиции инструмента в положении α3. При этом линейная скорость движения зерен абразива составляет V0 и происходит воздействие инструмента опять по мягкому направлению α. При перемещении оси α в положение траектории α1 движения зерен абразива обрабатывающего инструмента также меняют кристаллографическую направленность относительно неподвижной обрабатываемой октаэдрической поверхности алмаза. Траектории движения зерен абразива инструмента С1 в этом случае совпадают с твердым направлением b1 поверхности октаэдра на рис. 7.2. Величина линейной скорости V1 при этом увеличивается относительно V0, поскольку увеличивается радиус движения зерен абразива инструмента на величину гa. |
 Вернуться к просмотру книги
Вернуться к просмотру книги
 Перейти к Оглавлению
Перейти к Оглавлению
 © 2020 LoveRead.ec - электронная библиотека в которой можно
© 2020 LoveRead.ec - электронная библиотека в которой можно