Величайшие математические задачи - читать онлайн книгу. Автор: Йен Стюарт cтр.№ 88

При подсчете количества решений полиномиального уравнения иногда бывает удобно учесть одну и ту же точку несколько раз. Можно сказать, что совокупность решений состоит из множества точек, за каждой из которых мы «закрепляем» число, соответствующее его кратности. Можно, к примеру, иметь решения 0, 1 и 2 с кратностью 3, 7 и 4 соответственно. Многочлен в этом случае будет x³(x − 1)⁷(x − 2)⁴, если вам это интересно. Каждая из трех точек x = 0, 1 или 2 является (достаточно тривиальным) подмногообразием множества комплексных чисел. Поэтому решения этого полиномиального уравнения можно описать как список из трех подмногообразий с прикрепленным к каждому из них целым числом (вроде этикетки).

Алгебраический цикл выглядит примерно так же. Вместо отдельных точек мы можем использовать любой конечный список подмногообразий, присоединив к каждому из них числовую метку, не обязательно целую. Меткой может быть отрицательное целое число, рациональное число, действительное или даже комплексное число. По разным причинам в гипотезе Ходжа в качестве меток используются рациональные числа, о чем свидетельствует формулировка «рациональная линейная комбинация». К примеру, в качестве первоначального многообразия может выступать единичная сфера в 11-мерном пространстве; тогда список, о котором идет речь, мог бы выглядеть так:

• семимерная гиперсфера (задаваемая такими-то уравнениями) с меткой 22/7;

• тор (задаваемый такими-то уравнениями) с меткой −4/5;

• кривая (задаваемая такими-то уравнениями) с меткой 413/6.

Не пытайтесь это представить или, если очень захочется, нарисуйте картинку в стиле комикса: три бесформенные кляксы с надписями. Каждая такая картинка, каждый список представляет один алгебраический цикл.

К чему устраивать такой шум и изобретать подобные абстракции? К тому, что они отражают самые существенные аспекты первоначального алгебраического многообразия. Специалисты по алгебраической геометрии заимствуют методы у топологов.

В главе 10, где речь шла о гипотезе Пуанкаре, мы говорили о муравье, вселенной которого является поверхность. Как может муравей определить форму своей вселенной, если он не в состоянии отойти в сторонку и посмотреть? В частности, как он сможет отличить сферу от тора? Представленное в той главе решение предусматривало использование замкнутых кривых — топологических автобусных маршрутов. Муравей перемещает эти петли по всей поверхности, выясняет, что происходит, если поставить их одну за другой — концом к началу, и вычисляет алгебраический инвариант пространства, известный как его фундаментальная группа. Слово «инвариант» означает, что топологически эквивалентные пространства имеют одну и ту же фундаментальную группу. Если группы различны, то различны и пространства. Именно этот инвариант привел Пуанкаре к его гипотезе. Однако бедному муравью непросто проверить все возможные в его вселенной маршруты, и это замечание отражает реальные математические тонкости в расчетах фундаментальных групп. Существует и более практичный инвариант, Пуанкаре его тоже исследовал. Процесс перемещения петель по поверхности называется гомотопией; альтернативный вариант называется похоже, но иначе — гомологией.

Я покажу вам простейший, самый конкретный вариант гомологии. Топологи быстро развили этот вариант, оптимизировали и обобщили его, превратив в мощнейшую математическую машину, которая получила название «гомологическая алгебра». Этот простой вариант позволит вам лишь слегка почувствовать, как все это работает, но ведь нам ничего больше и не нужно.

Муравей начинает с того, что обследует свою вселенную и составляет карту. Подобно любому профессиональному топографу, он покрывает вселенную сетью треугольников. Главное при этом — чтобы ни в одном треугольнике не оказалось дырки в поверхности. Проще всего обеспечить это, вставляя каждый треугольник в виде резиновой заплатки, как при ремонте велосипедной камеры. При этом каждый треугольник будет иметь хорошо определенную внутренность, топологически эквивалентную внутренности любого обычного треугольника на плоскости. Топологи называют такую треугольную заплатку топологическим диском, поскольку она эквивалентна кругу. Чтобы убедиться в этом, взгляните на рис. 36 в главе 10, где треугольник постепенно модифицируется в круг. Подобную заплатку невозможно поставить поверх отверстия, потому что отверстие создает туннель, связывающий внутреннюю часть треугольника с его внешней частью. Чтобы перекрыть отверстие, заплатке придется выйти за пределы поверхности, а муравью запрещено делать это.

Итак, муравей провел триангуляцию своей вселенной. Условие про заплатку гарантирует, что, имея полный список треугольников и зная, какой треугольник с какими граничит, можно восстановить топологию поверхности, т. е. ее форму в смысле топологической эквивалентности. Если бы можно было поехать в «Икею» и купить Универсальный муравьиный набор надлежащим образом промаркированных треугольников, то мы могли бы, склеив аккуратно сторону А со стороной АА, сторону В со стороной ВВ и т. д., построить соответствующую поверхность. Сам муравей заперт на этой поверхности и потому не может построить ее модель, но он может быть уверен, что в принципе его карта содержит всю необходимую для построения информацию. Чтобы извлечь эту информацию, муравью придется проводить вычисления. При этом ему придется рассматривать уже не бесконечное число возможных петель, но все же достаточно большое их число: все замкнутые петли, проходящие вдоль ребер выбранной им сетки.

В гомотопии мы задаемся вопросом, можно ли сжать данную петлю непрерывно в точку. В гомологии мы задаемся другим вопросом: образует ли данная петля границу топологического диска? Иными словами, можно ли взять одну или несколько треугольных заплаток вместе таким образом, чтобы в сумме получился участок без отверстий с замкнутой границей?

На рис. 47 слева показана часть триангуляционной сети сферы — замкнутая петля и топологический диск, границей которого она является. Применив подходящие методики, можно доказать, что любая петля в триангуляционной сети сферы является такой границей: треугольные заплатки, а в более общем случае топологические диски, — это детекторы отверстий, а интуитивно понятно, что в сфере отверстий нет. Однако в торе отверстие имеется и в самом деле некоторые петли на торе не являются границами таких областей. На рис. 47 справа показана такая петля, проходящая сквозь центральное отверстие. Иными словами: просмотрев список петель и проверив, какие из них являются границами непрерывных областей, муравей может отличить сферическую вселенную от тороидальной.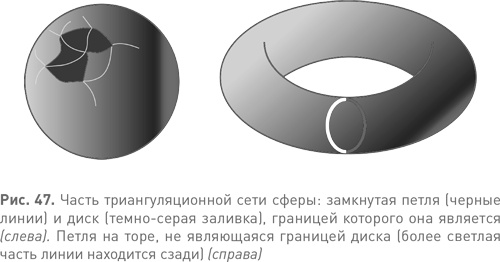

Если наш муравей столь же умен, как Пуанкаре и другие топологи того времени, он сможет превратить эту идею в элегантный топологический инвариант — гомологическую группу своей поверхности. Базовая идея заключается в том, чтобы «сложить» две петли, нарисовав их обе. Однако то, что получилось, не является петлей, поэтому нам придется вернуться и начать заново. Более того, вернуться нам придется в самое начало, в те дни, когда мы только начинали свое знакомство с алгеброй. Моя учительница математики для начала поведала нам, что можно сложить количество яблок в одной кучке с количеством яблок в другой и получить общее количество яблок. Но нельзя сложить яблоки с апельсинами — разве что если хотите узнать общее число фруктов.