Величайшие математические задачи - читать онлайн книгу. Автор: Йен Стюарт cтр.№ 66

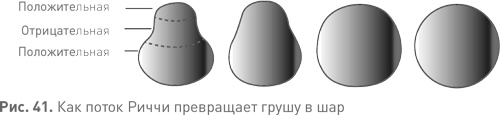
В этом примере топологический тип поверхности был очевиден с самого начала, однако та же общая стратегия действует для любого многообразия. Начните со сложной формы и следуйте за потоком Риччи. Со временем кривизна перераспределяется более равномерно, и форма упрощается. В конце концов вы должны получить простейшую форму с той же топологией, что и у первоначального многообразия, какой бы эта топология ни была. В 1981 г. Гамильтон доказал, что такая стратегия работает в двух измерениях, обеспечивая новое доказательство теоремы о классификации для поверхностей.

Кроме того, он добился значительного прогресса в аналогичной стратегии для трехмерных многообразий, но здесь возникло серьезное препятствие. В двух измерениях любая поверхность автоматически упрощается, следуя потоку Риччи. Это верно и в трех измерениях, если первоначальное многообразие во всех точках имеет строго положительную кривизну и нигде — нулевую или отрицательную. К несчастью, если в многообразии есть точки с нулевой кривизной — а они часто есть, — пространство, двигаясь в потоке, может запутаться. При этом возникают сингулярности — места, где многообразие перестает быть гладким. В таких точках уравнение потока Риччи не работает, и перераспределение кривизны прекращается. Естественный способ обойти это препятствие заключается в том, чтобы понять, что представляют собой сингулярности, и изменить многообразие — может быть, разрезать его на куски, чтобы можно было дать стартовый толчок потоку Риччи. Такая стратегия может оказаться успешной, если вы в достаточной степени контролируете связь топологии измененного многообразия к первоначальной. К несчастью, Гамильтон понял также, что для трехмерных пространств сингулярности потока Риччи могут быть чрезвычайно сложными — судя по всему, слишком сложными, чтобы применять подобные уловки. В общем, поток Риччи быстро стал в геометрии стандартным методом, но для доказательства гипотезы Пуанкаре его не хватило.

К 2000 г. гипотеза по-прежнему оставалась не доказанной; после вхождения в число семи проблем тысячелетия она приобрела еще более широкую известность и признание. К тому моменту стало ясно, что если каким-то образом удастся все же добиться, чтобы идея Гамильтона сработала, то тем самым будет доказана не только гипотеза Пуанкаре, но и гипотеза Терстона о геометризации. Приз был соблазнителен и близок, но в руки не давался.

В математике, как и в остальных отраслях науки, работа, чтобы ее признали, должна быть опубликована, а для этого — пройти рецензирование. Специалисты в соответствующей области должны внимательно прочитать работу, проверить логические выкладки и убедиться в безошибочности вычислений. Для сложной и значительной математической работы этот процесс может занять немало времени. Как упоминалось в главе 4, раньше выходом в каких-то ситуациях становился препринт, но сегодня существует стандартный веб-сайт arXiv.org, своеобразный архив, где после частичного рассмотрения и утверждения (чтобы отсечь всякие глупости) разрешается размещать электронные препринты. В настоящее время большинство исследователей знакомится с новыми результатами на сайте arXiv или на собственном сайте автора.

В 2002 г. Григорий Перельман разместил на сайте arXiv препринт о потоке Риччи. В работе было сделано замечательное утверждение: поток Риччи градиентоподобен. Иными словами, существует вполне определенное направление вниз — единственная числовая величина, связанная с формой многообразия, и многообразие всегда течет вниз в том смысле, что эта величина всегда уменьшается со временем. Она чем-то напоминает высоту в ландшафте и позволяет количественно оценить «упрощение» многообразия. Градиентоподобные потоки имеют немало ограничений: к примеру, они не могут ходить кругами или вести себя хаотично. Никто, похоже, не подозревал, что поток Риччи окажется таким ручным. Но Перельман не просто выдвинул предположение: он доказал это. В конце он наметил цепочку рассуждений, которые должны были бы доказать гипотезу Терстона о геометризации — а она, если помните, подразумевает гипотезу Пуанкаре, но заходит на самом деле гораздо дальше, — и пообещал подробнее изложить все это в следующих статьях на сайте arXiv. В течение следующих восьми месяцев он разместил там две статьи, содержавшие большую часть обещанных подробностей.

Первая статья вызвала немалый переполох. Перельман утверждал, что ему удалось реализовать всю программу Гамильтона — использовать поток Риччи для упрощения трехмерного многообразия и доказать, что результат получился в точности таким, как предсказывал Терстон. Две другие статьи добавили рассуждениям Перельмана убедительности: у математиков возникло чувство, что это человек знает, о чем говорит, и что его идеи — не просто очередная правдоподобная стратегия с неизменной логической прорехой или недоказанным допущением. Обычный скепсис математического сообщества по отношению к любым заявлениям о решении одной из великих задач слегка поутих. Возникло ощущение, что его попытка вполне может увенчаться успехом.

Однако дьявол, как всегда, кроется в деталях, а в математике детали бывают дьявольски непокорными! Работу необходимо было проверить, не спеша и на полную глубину, причем сделать это должны были те, кто разбирается в соответствующих областях и в состоянии распознать потенциальные ловушки. А это было непросто, поскольку Перельман в своей работе свел воедино по крайней мере четыре очень разные области математики и математической физики, а мало кто из математиков может похвастать знаниями более чем в одной-двух областях. Анализ корректности его доказательства потребовал бы много усилий и командной работы. Более того, в препринтах на сайте arXiv не было всех подробностей, необходимых в публикуемой статье. Для препринтов они были написаны довольно ясно, но точки над i там были расставлены не все. Так что экспертам нужно было реконструировать часть рассуждений Перельмана — при том, что сам-то он занимался этой работой несколько лет!

На все это требовалось время. Перельман читал лекции по своему доказательству и отвечал по электронной почте на вопросы, касавшиеся различных его этапов. Всякий раз, как кто-нибудь находил кажущуюся прореху, он быстро откликался, объяснял необходимое и заполнял пробелы. Все выглядело обнадеживающе. Однако никто не собирался рисковать репутацией и заявлять публично, что Перельман доказал гипотезу Пуанкаре и, тем паче, еще более сложную гипотезу о геометризации. Нужна была полная уверенность в том, что доказательство безошибочно. Поэтому, несмотря на общее благосклонное отношение к работе Перельмана, публичного признания она поначалу не получила. Это было ожидаемо, но время шло, и Перельмана все больше охватывало раздражение, потому что, как ему казалось, он впустую тратил время. Он-то знал, что его доказательство верно, и не мог понять, почему у остальных возникают такие сложности. Он отказался написать о своей работе подробнее или представить статью в какой-нибудь журнал. С его точки зрения, дело было сделано, а препринты на arXiv содержали всю необходимую информацию. Он перестал отвечать на вопросы, касавшиеся недостающих вроде бы деталей. Для него все было очевидно. Да ладно, ребята, вы и сами можете разобраться в этом, без моей помощи. Это не так уж сложно.