Величайшие математические задачи - читать онлайн книгу. Автор: Йен Стюарт cтр.№ 38

Это уравнение можно рассматривать в нескольких различных контекстах, в зависимости от того, какие ограничения наложены на переменные и коэффициенты. Если все это действительные числа, уравнение определяет кривую на плоскости. Если это комплексные числа, то специалисты по алгебраической геометрии все равно называют множество решений этого уравнения кривой просто по аналогии. Но теперь это кривая в пространстве пар комплексных чисел, четырехмерном в действительных координатах. И кривая в данном случае — это поверхность с точки зрения действительных координат.

На рис. 27 показаны типичные действительные эллиптические кривые y² = 4x³ − 3x + 2 и y² = 4x³ − 3x. Поскольку y появляется в уравнении в виде квадрата, кривая симметрична относительно горизонтальной оси. В зависимости от коэффициентов это либо одна волнообразная кривая, либо кривая с отдельным овальным компонентом. В комплексных числах кривая всегда представляет собой единое связное множество.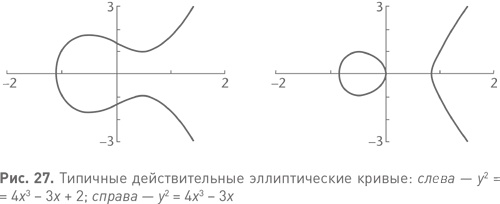

Если мы потребуем, чтобы переменные и коэффициенты были рациональными, в игру вступит теория чисел и мы получим диофантово уравнение. Его графическое представление зачем-то называется эллиптической кривой, хотя совершенно не похоже на эллипс. Все дело в том, что это уравнение связано с эллиптическими функциями. Это как назвать окружность треугольной кривой только потому, что она связана с тригонометрией. Однако это название уже высечено на скрижалях, так что нам придется мириться с ним.

Теория эллиптических функций — глубокая и богатая теория, математики открыли у эллиптических кривых бессчетное количество красивых свойств. Одно из них аналогично тому, как мы объединяем два решения пифагорова уравнения, складывая соответствующие углы и получая третье решение. Две точки на эллиптической кривой можно «сложить», проведя через них прямую линию и посмотрев, в какой точке она пересечет кривую в третий раз (см. рис. 28). (Заметим, что третья точка обязательно существует, поскольку уравнение кубическое. Однако она может оказаться «в бесконечности» или совпасть с одной из первых двух точек, если прямая пройдет по касательной к кривой.) Если первые две точки у нас обозначены как P и Q, обозначим третью как P*Q.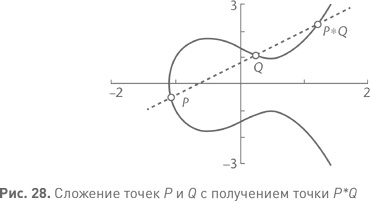

Расчет показывает, что если P и Q — рациональные точки, то и точка P*Q рациональна. Операция * придает набору рациональных точек алгебраическую структуру, но оказывается полезной и при рассмотрении еще одной связанной с этим операции. Выберем любую рациональную точку O на кривой и определим:

Эта новая операция подчиняется некоторым фундаментальным законам обычной алгебры, причем O ведет себя как нуль и превращает множество всех рациональных точек в то, что специалисты по алгебре называют группой (см. главу 10). Важно, что здесь, как с пифагоровыми тройками, можно «сложить» любые два решения и получить третье. То, что «групповой закон» действует на рациональные точки, поразительно: в частности, это означает, что стоит нам найти два рациональных решения диофантова уравнения, и мы автоматически получим множество других решений.

Около 1908 г. Пуанкаре задался вопросом: существует ли конечный набор решений, такой, чтобы из него можно было получить все остальные решения последовательным применением групповой операции? Это важно, потому что из существования такого набора следует, что все рациональные решения можно охарактеризовать при помощи конечного списка решений. В интереснейшей работе 1922 г. Морделл доказал, что ответ на вопрос Пуанкаре положителен. После этого эллиптические кривые стали центральным элементом теории чисел, поскольку далеко не все диофантовы уравнения могут похвастать такой степенью контроля. Итак, эллиптические кривые, как и пифагорово уравнение, имеют бесконечное множество рациональных решений. Многие диофантовы уравнения, напротив, имеют конечное число или вообще не имеют решений. Я собираюсь немного отклониться от темы и поговорить о целом семействе подобных уравнений и полученном недавно замечательном доказательстве того, что существуют лишь очевидные решения.

Пифагорейцы были увлечены своим уравнением, потому что верили: в основе Вселенной лежат числа. В поддержку этой философии они обнаружили, что музыкальной гармонией управляют простые числовые отношения. Это было установлено экспериментально при помощи наблюдений за звучанием натянутой струны. Струна с такой же степенью натяжения, но вдвое меньшей длины, дает ноту на октаву выше. Это самое гармоничное сочетание двух нот — настолько гармоничное, что звучит даже несколько простовато. В западной музыке следующая по значению гармония — кварта, где одна струна по длине составляет 3/4 другой струны, и квинта, где длина одной струны составляет 2/3 от длины другой.

Начав с 1 и умножая последовательно на 2 или 3, можно получить числа 2, 3, 4, 6, 8, 9, 12 и т. д. — числа вида 2^a3^b. Благодаря связи с музыкой они получили название гармонических. В XIII в. во Франции еврейский ученый по имени Гершон бен Соломон Каталан написал книгу «Врата небес», посвятив три ее части физике, астрономии и метафизике. В 1343 г. епископ Мо убедил его сына (по крайней мере историки считают, что, вероятно, это был его сын) Леви бен Гершома написать математическую книгу «Гармония чисел». В нее вошла, в частности, задача, которую впервые поставил композитор и теоретик музыки Филипп де Витри: когда два гармонических числа могут различаться на единицу? Подобные пары найти несложно: сам де Витри знал их четыре: (1, 2), (2, 3), (3, 4) и (8, 9). Но Гершом доказал, что это все возможные решения и других не существует.

Среди перечисленных де Витри пар гармонических чисел наибольший интерес привлекает пара (8, 9). Первое число в ней — куб, 2³; второе — квадрат, 3². Математики заинтересовались, могут ли другие квадраты и кубы различаться на единицу; Эйлер доказал, что не могут, за исключением тривиального случая (0, 1) и случая (−1, 0), если разрешены отрицательные числа. В 1844 г. уже другой Каталан опубликовал более всеобъемлющее заявление, о котором, должно быть, думали многие математики, но которое никто до него не счел нужным озвучить. Речь идет о бельгийском математике Эжене Шарле Каталане, который в 1844 г. написал в один из ведущих математических журналов того времени Journal für die Riene und Angewandte Mathematik следующее: