Величайшие математические задачи - читать онлайн книгу. Автор: Йен Стюарт cтр.№ 19

Уже 200 лет математики считают комплексные числа фундаментальной концепцией своей науки. Мы сегодня признаем, что логически комплексные числа имеют ту же основу, что и более знакомые «действительные» — ведь те тоже, подобно всем математическим структурам, представляют собой абстрактное понятие, а не реальную физическую вещь. Комплексные числа широко использовались еще до Гаусса, но их статус оставался неясным, пока Гаусс и другие математики не сорвали с них завесу тайны, раскрыв неожиданную и парадоксальную причину их привлекательности: несмотря на загадочность и неясный смысл, комплексные числа ведут себя гораздо лучше действительных. Они внесли недостающую составляющую, которой не хватало действительным числам, — обеспечили любому алгебраическому уравнению полный набор решений.

Простейший пример — квадратные уравнения. Одни из них имеют по два действительных решения, другие — не имеют ни одного. К примеру, решениями уравнения x² − 1 = 0 являются 1 и −1, а уравнение x² + 1 = 0 решений не имеет. Промежуточное положение занимает x² = 0, единственное решение которого равно 0, но в некотором смысле это единственное решение «повторяется дважды» ^{11}. Если же мы разрешим комплексные решения, то окажется, что x² + 1 = 0 тоже имеет два решения: i и — i. Гаусс не стеснялся пользоваться комплексными числами; мало того, его докторская диссертация содержала первое логически безупречное доказательство фундаментальной теоремы алгебры: число комплексных решений любого полиномиального уравнения (если корректно посчитать кратные корни) равняется степени уравнения. Поэтому квадратные уравнения (второй степени) всегда имеют по два комплексных решения, кубические (третьей степени) — по три и т. д.

Уравнение x⁵ − 1 = 0, определяющее, как я уже сказал, правильный пятиугольник, — это уравнение пятой степени, поэтому и комплексных решений у него пять. Действительное решение одно: x = 1. Где же остальные четыре? Они представляют собой четыре вершины правильного пятиугольника на комплексной плоскости, притом что x = 1 — это пятая вершина (см. рис. 7, справа). Это соответствие — удачный пример математической красоты: элегантная геометрическая фигура становится элегантным уравнением.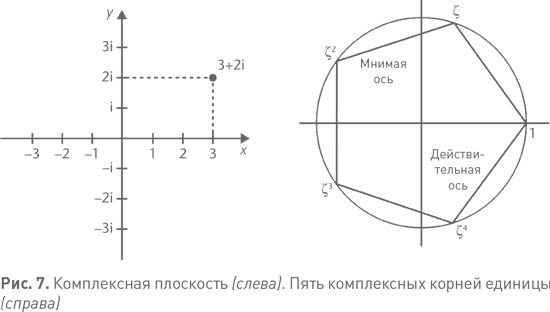

Вспомним, однако, о том, что эти пять точек являются решениями уравнения пятой степени, а 5 — это не степень двойки. Но, как уже говорилось, уравнение пятой степени раскладывается на две части со степенями 1 и 4; эти части называют его неприводимыми делителями.

(«Неприводимость» означает, что у этих многочленов уже нет делителей, как у простых чисел.) Первый делитель дает единственное действительное решение x = 1. Второй делитель дает четыре комплексных решения — и четыре вершины пятиугольника. Так что с комплексными числами все выглядит гораздо разумнее и элегантнее.

Часто сложно понять, каким путем математики прошлого приходили к новым открытиям, потому что в те времена было принято представлять только конечный результат размышлений и оставлять в стороне все ошибочные шаги, которые были сделаны в ходе исследования. Эта проблема часто осложняется и тем, что естественный ход мысли в прошлом выглядел иначе, чем сегодня. Гаусс, в частности, широко известен своей склонностью заметать следы и публиковать только конечный, тщательно отшлифованный анализ. Однако в том, что касается исследований Гаусса по построению 17-угольника, материала у нас достаточно: окончательная публикация содержит достаточно ценных указаний.

Его отправная точка новизной не отличалась. И до Гаусса кое-кто из математиков понимал, что приведенный выше анализ правильных многоугольников работает в общем случае. Построение многоугольника с числом сторон n эквивалентно решению уравнения xⁿ − 1 = 0 в комплексных числах. Более того, этот многочлен раскладывается на два многочлена вида

Опять же первый множитель дает действительное решение x = 1, а остальные n − 1 решений получаются из второго множителя. Если n нечетное, все они комплексные; если n четное, одно из них становится вторым действительным решением x = −1.

Однако Гаусс заметил то, что просмотрели все остальные: иногда второй делитель можно выразить через несколько квадратных уравнений. Не представить в виде произведения более простых множителей, поскольку это невозможно, а решить с использованием уравнений, коэффициенты которых решают другие уравнения. Ключевым фактором — слабым звеном всей задачи — является одно элегантное свойство алгебраических уравнений, возникающее, когда мы решаем их подобным образом одно за другим. Такой расчет всегда эквивалентен решению единственного уравнения, но, как правило, более высокой степени. Повышение степени — цена, которую мы платим за уменьшение количества уравнений. Технически эта процедура может оказаться достаточно сложной и путаной, но одно мы можем предсказать заранее: какая получится степень. Для этого достаточно перемножить степени всех последовательных многочленов.

Если все они квадратные, то результат будет 2 × 2 × … × 2, т. е. степень двойки. Поэтому, если построение существует, n − 1 должно быть степенью двойки. Однако этого условия не всегда достаточно. Если n = 9, n − 1 = 8, а это степень двойки. Но Гаусс выяснил, что для правильного девятиугольника построения не существует, поскольку 9 — не простое число ^{12}. А как насчет следующего шага, на котором мы решаем систему из четырех квадратных уравнений? Степень n − 1 соответствующего объединенного уравнения равна 2 × 2 × 2 × 2 = 16. Тогда n = 17, а это простое число.