Величайшие математические задачи - читать онлайн книгу. Автор: Йен Стюарт cтр.№ 15

К примеру, мы знаем, что существует бесконечно много простых чисел вида 4k + 1 и 4k + 3. В более общем виде это утверждение выглядит так: любая арифметическая прогрессия ak + b с постоянными параметрами a и b содержит бесконечно много простых чисел, если a и b не имеют общих делителей. К примеру, пусть a = 18. Тогда b = 1, 5, 7, 11, 13 или 17. Следовательно, существует бесконечно много простых чисел видов 18k + 1, 18k + 5, 18k + 7, 18k + 11, 18k + 13 или 18k + 17. Но это неверно для 18k + 6, например, потому что 18 кратно 6. Ни одна арифметическая прогрессия не может состоять только из простых чисел, но недавний серьезный прорыв — теорема Грина — Тао — показывает, что последовательность простых чисел содержит арифметические прогрессии произвольной длины. В 2004 г. Бен Грин и Теренс Тао разработали очень глубокое и сложное доказательство этого утверждения, что внушает надежду: на самые сложные вопросы, какими бы неприступными они ни выглядели, в конце концов может быть получен ответ.

Снимаем шляпу, а потом надеваем ее — и вновь за работу: мы немедленно задаемся вопросом о более сложных формулах с k. Не существует простых чисел вида k²; не существует и простых вида k²−1, за исключением 3, поскольку подобные выражения раскладываются на множители. Однако выражение k² + 1 не имеет очевидных делителей, и простых чисел такого вида можно найти множество:

Можно привести пример и с бо́льшими цифрами, хотя особого смысла в этом нет:

Предполагается, что таких простых чисел тоже бесконечно много, но до сих пор не доказано ни одного подобного утверждения ни для одного конкретного многочлена, в котором k стояло бы в степени выше единицы. Очень правдоподобное предположение сделал в 1857 г. Виктор Буняковский: любой многочлен от k, не имеющий очевидных делителей, представляет бесконечное множество простых чисел. Исключение составляют не только разложимые многочлены, но и такие многочлены, как k² + k + 2 (этот многочлен всегда делится на 2, хотя и не имеет алгебраических делителей).

Некоторые многочлены, судя по всему, обладают особыми свойствами. Классический пример: k² + k + 41. Этот простое число, если k = 0, 1, 2, …, 40 и, строго говоря, если k = −1, −2, …, — 40 тоже. Длинные цепочки простых чисел при последовательных значениях k попадаются редко, и о них мы кое-что знаем. Но в целом вся эта область весьма загадочна.

Гипотеза о парах простых чисел почти так же знаменита, как гипотеза Гольдбаха, и, судя по всему, столь же неприступна. Вот ее суть: существует бесконечно много пар простых чисел с разницей в 2. Приведем несколько примеров:

На сегодняшний день (на январь 2012 г.) наибольшими известными парными простыми являются числа 3 756 801 695 685 × ^{2666 669} ± 1, содержащие по 200 700 десятичных знаков. Они были найдены в 2011 г. в рамках проекта распределенных вычислений PrimeGrid. В 1915 г. Вигго Брун при помощи одного из вариантов решета Эратосфена доказал, что сумма чисел, обратных всем парным простым, сходится, в отличие от суммы чисел, обратных всем простым. В этом смысле парные простые встречаются относительно редко. При помощи аналогичных методов он доказал также, что существует бесконечно много целых n, таких, что n и n + 2 имеют не больше девяти простых делителей. Харди и Литлвуд при помощи своих эвристических методов пришли к выводу, что количество пар простых, меньших x, асимптотически приближается к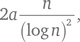

где a — константа, равная приблизительно 0,660161. Идея в том, что в данном случае можно считать простые числа возникающими случайно с частотой, которая делает общее число простых вплоть до x приблизительно равным x/log x. Аналогичных гипотез и эвристических формул существует множество, но строгих доказательств для них опять же не существует.

Да, в математике есть сотни открытых вопросов, имеющих отношение к простым числам. Одни из них просто любопытны, другие глубоки и имеют большую важность. С некоторыми вопросами из последней категории нам еще предстоит встретиться в главе 9. Ведь несмотря на все успехи математики за последние 2500 лет, скромные простые числа не потеряли ни своей притягательности, ни загадочности.

Простые числа известны давно, но круг — еще более древнее понятие. И именно он породил великую задачу, на решение которой ушло больше 2000 лет. Речь идет об одной из взаимосвязанных геометрических задач, корни которых уходят глубоко в античные времена. Главное действующее лицо этой истории — число π (греческая буква «пи»), знакомое нам по школьной программе в связи с окружностями и сферами. Численно это число равно 3,14159 и еще чуть-чуть; нередко также используется приблизительное значение 22/7. Десятичные знаки в записи π никогда не заканчиваются и не повторяются в одной и той же последовательности снова и снова. Нынешний рекорд вычисления точного значения числа π составляет 10 трлн знаков после запятой. Этот результат Александр Йи и Шигеру Кондо опубликовали в октябре 2011 г. Расчеты такого рода важны как способ испытания быстрых компьютеров или новых, еще более хитроумных методик вычисления числа π, но от численного результата как такового почти ничего не зависит. Причина интереса к числу π не в том, что без него невозможно вычислить длину окружности. Это странное число то и дело мелькает в самых разных областях математики, причем не только в формулах, имеющих отношение к кругам и сферам, и заводит в невероятные дебри. Тем не менее школьные формулы тоже важны, к тому же они отражают древнегреческое происхождение π.

Там одной из величайших проблем считалась нерешенная задача о квадратуре круга. В современном языке эта фраза часто используется иносказательно и означает безнадежное, бессмысленное или тщетное предприятие. Как многие общеупотребительные фразы, берущие начало в научной терминологии, эта с течением времени не раз меняла значение ^{5}. В греческие времена попытка найти квадратуру круга представлялась вполне разумным начинанием. Разница формы этих фигур — прямые или изогнутые границы — никакого значения не имеет: многие аналогичные задачи решаются ^{6}. Однако со временем выяснилось, что эта конкретная задача не может быть решена заданными методами. Чтобы это доказать, пришлось проявить изобретательность и сделать серьезные теоретические выкладки, но общую идею доказательства понять все же можно.