Истина и красота. Всемирная история симметрии - читать онлайн книгу. Автор: Йен Стюарт cтр.№ 87

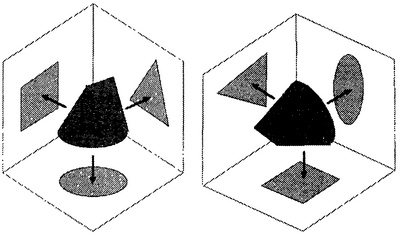
Теперь представим себе флатландца, живущего на «полу» моего рисунка, так что ему видна проекция пробки на пол, но он и не подозревает о других проекциях. В один прекрасный день он, к своему изумлению, обнаруживает, что круглая форма каким-то образом изменилась и стала квадратом. Как такое может быть? Это определенно не симметрия.

Не симметрия — да, во Флатландии. Но когда флатландец отвернулся, кто-то, живущий в трехмерии, повернул пробку так, что ее проекция на пол превратилась в квадрат. При этом в трехмерии вращение является преобразованием симметрии ^[106]. Так что симметрия в более высокой размерности может иногда объяснить совершенно непостижимое преобразование в более низкой размерности.

Нечто очень похожее происходит в суперсимметрии, но вместо превращения окружности в квадрат фермионы там превращаются в бозоны. Это удивительно. В самом деле, вы можете выполнить вычисления с фермионами, напустить на каждый операцию суперсимметрии и получить результат для бозонов без всяких дополнительных усилий ^[107]. Или наоборот.

Подобного мы ожидаем от настоящих симметрий. Если вы стоите перед зеркалом и жонглируете мячиками, то все происходящее с вашей стороны зеркала полностью определяет происходящее с другой стороны. Ваш образ там жонглирует образами мячиков. Если выполнение последовательности приемов занимает 3,79 с с этой стороны зеркала, то без всяких измерений ясно, что выполнение той же последовательности приемов займет 3,79 с с другой стороны. Две ситуации связаны зеркальной симметрией; что бы ни происходило с одной стороны, оно происходит также и в отражении.

Суперсимметрии не настолько просты, но приводят к похожему эффекту. Они позволяют вывести свойства частиц одного типа из свойств частиц совершенно иного типа. Дело обстоит почти так же, как если бы вы могли забраться куда-то в высокомерную область вселенной и там повернуть фермион, превратив его в бозон. Частицы организуются в суперсимметричные пары: обычной частице отвечает ее повернутая версия, называемая счастицей. Электроны имеют в паре с собой сэлектроны, кварки — скварки. По историческим причинам близнец фотона называется не сфотон, а фотино. Имеется своеобразный «теневой мир» счастиц, который только слабо взаимодействует с обычным миром.

В ногу с этой идеей идет изящная математика, но массы этих предсказываемых теневых частиц слишком велики для того, чтобы их можно было наблюдать в экспериментах ^[108]. Суперсимметрия прекрасна, но может не быть истинной. Но даже если вопрос не состоит в прямом подтверждении, вполне возможными могут оказаться подтверждения косвенные. Наука проверяет теории главным образом через их следствия.

Виттен активно развивал суперсимметрию и в 1984 году написал статью, озаглавленную «Суперсимметрия и теория Морса». Теория Морса — это область топологии, названная по имени своего первоисследователя Марстона Морса, в которой устанавливается связь общей формы некоторого пространства с его пиками и долинами. Сэр Майкл Атья — вероятно, наиболее крупный из ныне здравствующих британских математиков — считает, что статья Виттена представляет собой «обязательное чтение для геометров, заинтересованных в понимании современной квантовой теории поля. Она также содержит блестящее доказательство классического неравенства Морса. Реальная цель статьи состоит в подготовке почвы для суперсимметричной квантовой теории поля в терминах бесконечномерных многообразий». В дальнейшем Виттен применил эти методы к другим актуальным вопросам на дальних рубежах топологии и алгебраической геометрии.

Должно быть понятно, что, когда я сказал, что Виттен не математик, я не имел в виду отсутствие у него математического таланта. Как раз наоборот — быть может, ни у кого на планете нет большего математического таланта. Но в случае Виттена к этому добавляется удивительная физическая интуиция.

В отличие от математиков физики редко стесняются использовать физическую интуицию, чтобы перескочить через пробел в математической логике. Математики же привыкли относиться к «мостам веры» с подозрением вне зависимости от того, сколь много имеется подтверждающих свидетельств: для математиков доказательство — это все. Виттен необычен в том отношении, что он может соотносить свою интуицию с той математикой, которая понятна математикам. Атья выражает это такими словами: «Его способность интерпретировать физические идеи в математических терминах совершенно уникальна. Снова и снова он удивляет математическое сообщество своими блестящими физическими озарениями, приводящими к новым глубоким математическим теоремам».

Но у этой интуитивной мощи есть и оборотная сторона. Многие из важнейших Виттеновых идей, выведенных из физических принципов или аналогий, появились без доказательств, а в отношении некоторых доказательства отсутствуют и по сей день. Не в том дело, что он не может дать доказательства, — может, как показывает его Филдсовская медаль, — а в том, что он может делать логические скачки, ведущие к глубокой и верной математике, словно бы не нуждаясь в доказательствах.

Главный вопрос — имеет ли изящная виттеновская математика какое-нибудь отношение к фундаментальной физике? Или же поиски красоты завели в математический тупик, где потеряна всякая связь с физической истиной? К 80-м годам двадцатого века физики объединили три из четырех взаимодействий, имеющихся в природе: электромагнитное, слабое и сильное ^[109]. Но Теории Великого Объединения ничего не говорят о гравитации. Сила, которую мы наиболее непосредственно ощущаем в повседневной жизни, которая буквально не дает нам витать в облаках, исключена из синтеза — конфуз?

Достаточно несложно написать комбинированную теорию, включающую гравитацию и квантовую теорию и с виду выглядящую разумно. Но при всякой попытке решить получающиеся там уравнения возникает бессмыслица. Как правило, числа, призванные выражать разумные физические величины, оказываются бесконечными. Бесконечность в физической теории указывает: что-то идет не так. Именно появление бесконечности в законе излучения подтолкнуло Планка к квантованию света.