Истина и красота. Всемирная история симметрии - читать онлайн книгу. Автор: Йен Стюарт cтр.№ 47

Гамильтону повезло больше, чем Абелю или Галуа, в том отношении, что на его необычные способности обратили внимание в раннем детстве. Поэтому вполне естественно, что в 1823 году он поступил в ведущий ирландский университет — дублинский Тринити Колледж. Равным образом неудивительно, что он шел первым в списке из сотни кандидатов. Во время учебы в Тринити он получил все возможные награды. И, что еще важнее, он закончил первый том своего основополагающего труда по оптике.

Весной 1825 года Гамильтон открыл для себя притяжение прекрасного пола, представшего перед ним в лице Кэтрин Дизни. Наверное, он поступил не слишком мудро, ограничив свои знаки внимания написанием стихов, потому что его потенциальная возлюбленная недолго думая вышла замуж за священника старше ее на пятнадцать лет, который был способен на несколько менее литературный подход к порядочным девицам. Сердце Гамильтона было разбито; несмотря на свою твердую приверженность религиозным заповедям, он подумывал о том, чтобы утопиться, то есть совершить смертный грех. Однако здравомыслие одержало верх, и он излил свою разочарованную душу еще в одной поэме.

Гамильтон любил поэзию, и круг его друзей включал самых видных литераторов. Уильям Вордсворт стал его близким другом; он также часто встречался с Сэмюелем Тейлором Колриджем и другими писателями и поэтами. Вордсворт оказал Гамильтону ценнейшую услугу, деликатно намекнув ему, что его таланты лежат не в сфере поэзии:

Гамильтон ответил в том смысле, что его истинной поэзией была математика, и мудро переключился на научное поприще. в 1827 году, еще в бытность его студентом, Гамильтона единогласно избрали профессором астрономии в Тринити после того, как занимавший эту должность Джон Бринкли подал в отставку, а точнее, стал епископом Клойна. Гамильтон начал сразу с громкого успеха, опубликовав свою книгу по оптике — предмету, важному для астрономии, поскольку оптика лежит в основании устройства большинства астрономических инструментов.

Связь с механикой там присутствовала лишь в зачаточной форме. Основной фокус книги, если можно так выразиться, заключался в геометрии световых лучей — как они изменяют направление при отражении в зеркале или как преломляются в линзе. «Геометрическая оптика» позднее уступила место «волновой оптике», в которой свет рассматривается как волны. Волны обладают целым набором дополнительных свойств, самое заметное из которых — дифракция. Интерференция волн может приводить к размытию краев изображения и даже к эффекту, который выглядит как огибание светом угла (фокус, невозможный для лучей).

Геометрия световых лучей не была новым предметом; ее интенсивно изучали математики и до этого, начиная с Ферма и даже с греческого философа Аристотеля. Гамильтон сделал в оптике нечто подобное прославленному достижению Лежандра в механике: он избавился от геометрии и заменил ее алгеброй и анализом. А именно — заменил основанные на рисунках чисто геометрические рассуждения на абстрактные вычисления.

Это было существенным шагом вперед, поскольку неточные картинки, тем самым, заменялись строгим анализом. Позднее математики предприняли энергичные усилия, чтобы пройти путь, намеченный Гамильтоном, в обратном направлении и снова ввести в обиход наглядные образы. Но формальный алгебраический подход стал к тому моменту неотъемлемой частью математического мышления и мог оставаться естественным спутником более наглядных аргументов. Колесо моды сделало полный оборот, но на более высоком уровне, подобно спиральной лестнице.

Великим вкладом Гамильтона в оптику было объединение. Все огромное многообразие известных результатов он свел к одному фундаментальному методу. Вместо системы световых лучей он ввел одну-единственную величину, «характеристическую функцию» системы. С ее помощью любая оптическая конфигурация представлялась одним уравнением. Более того, это уравнение можно было решить единообразным способом, что давало полное описание всей системы лучей и ее поведения. Метод Гамильтона основывался на одном фундаментальном принципе: световые лучи, проходящие через любую систему зеркал, призм и линз, выбирают путь, распространение по которому до цели занимает наименьшее время.

Ферма еще ранее обнаружил некоторые специальные случаи этого принципа, назвав его принципом наименьшего времени. Простейший пример, позволяющий объяснить его работу, — это отражение света от плоского зеркала. Левый рисунок показывает, как световой луч, выходя из одной точки и отражаясь от зеркала, достигает второй точки. Одним из великих открытии на заре оптики был закон отражения, который гласит, что две части светового луча составляют с зеркалом равные углы ^[37].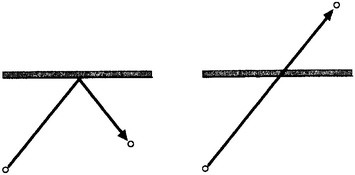

Ферма придумал изящный прием: отразить в зеркале второй участок луча, а заодно и вторую точку, как показано на правом рисунке. Благодаря Эвклиду условие «равных углов» — это то же самое, что утверждение, что в этой «отраженной» картине путь от первой точки до второй является прямой линией. Но Эвклид доказал тот знаменитый факт, что прямая линия есть кратчайшее расстояние между двумя точками. Поскольку скорость света в воздухе постоянна, кратчайшее расстояние означает то же самое, что наименьшее время.

Возвращаясь к геометрии на левом рисунке, мы видим, что выполнено то же самое утверждение. Таким образом, условие равных углов логически эквивалентно тому факту, что световой луч выбирает путь с наименьшим временем распространения из первой точки во вторую при условии, что по дороге надо отразиться от зеркала.

Связанный с этим принцип — закон преломления Снеллиуса — говорит о том, как «ломается» луч при переходе из воздуха в воду и вообще из одной среды в другую. Этот закон можно вывести подобным же образом, если учесть, что свет распространяется в воде медленнее, чем в воздухе. Гамильтон пошел еще дальше, утверждая, что тот же принцип минимизации времени применим ко всем оптическим системам, и воплотив эту мысль в едином математическом объекте — характеристической функции.

Использованная здесь математика впечатляла, но в руках Гамильтона она привела к немедленной экспериментальной отдаче. Гамильтон заметил, что из его метода следовало существование «конического преломления», когда один луч света при попадании на подходящий кристалл выходит из него в виде целого конуса лучей. В 1832 году это предсказание, неожиданное для всех кто работал в оптике, получило прочное экспериментальное подтверждение, когда Хэмфри Ллойд использовал кристалл арагонита. На следующее утро Гамильтон проснулся знаменитым.