Истина и красота. Всемирная история симметрии - читать онлайн книгу. Автор: Йен Стюарт cтр.№ 39

Однако Галуа смог доказать — просто изучая перестановки, — что такой нормальной подгруппы не существует.

Ладно, может быть, следует начать, скажем, с корня седьмой степени. Тогда 120 перестановок должны разбиться на семь блоков одного и того же размера — что невозможно, поскольку 120 не делится на 7. Значит, корня седьмой степени нет. На самом деле нет никаких корней простой степени, за исключением 2, 3 и 5, потому что именно таковы простые делители числа 120. А мы как раз исключили 5.

Что же тогда, начнем с кубического корня? К сожалению, не получится: группа из 120 перестановок не имеет нормальной подгруппы индекса 3.

Все, что осталось, — квадратный корень. Имеется ли в группе из 120 перестановок нормальная подгруппа индекса 2? Имеется, причем ровно одна. Она содержит 60 перестановок и называется знакопеременной группой. Так что, используя теорию групп Галуа, мы установили, что любая формула для решения общего уравнения пятой степени должна начинаться с квадратного корня, что приводит к знакопеременной группе. При первом ветвлении ствола появляются всего две ветви.

Но всего имеется 120 листьев, так что дерево должно и дальше как-то ветвиться. Как оно это делает? Простые делители числа 60 — это те же 2, 3 и 5. Так что каждая новая ветвь должна делиться на две, три или пять веточек. Другими словами, нам надо добавить или еще один квадратный корень, или кубический корень, или корень пятой степени. Более того, это можно сделать, если, и только если, знакопеременная группа содержит нормальную подгруппу индекса 2, 3 или 5.

Но содержит ли она такую нормальную подгруппу? Вопрос этот — целиком вопрос о перестановках на пяти символах. Исследуя такие перестановки, Галуа смог доказать, что в знакопеременной группе вообще нет нормальных подгрупп (за исключением всей группы и тривиальной подгруппы [I]). Это «простая» группа, одна из тех основных компонент, из которых можно построить все группы.

Не нашлось достаточного количества нормальных подгрупп, чтобы соединить ствол со всеми листьями при помощи ветвлений на простое число веток на каждом шаге. Так что процесс решения уравнения пятой степени в радикалах натыкается на внезапную остановку после того первого шага, заключающегося в добавлении квадратного корня. Идти больше некуда. Нет дерева, по которому можно было бы добраться от ствола до листьев, а потому нет формулы для корней в терминах радикалов.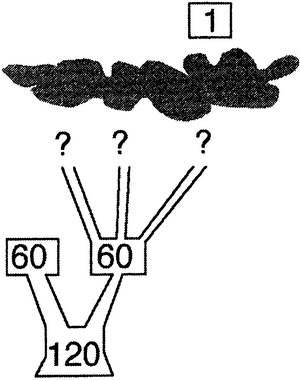

Та же идея работает для уравнений степени 6, 7, 8, 9 — любой степени, старшей 5. Теперь неизбежно возникает вопрос, а почему же уравнения второй, третьей и четвертой степени, тем не менее, разрешимы? Чем выделены степени 2, 3 и 4? В действительности теория групп точно говорит нам, как решить уравнения второй, третьей и четвертой степени. Я оставлю в стороне технические подробности, а вместо этого просто покажу как выглядят деревья. Они в точности соответствуют классическим формулам.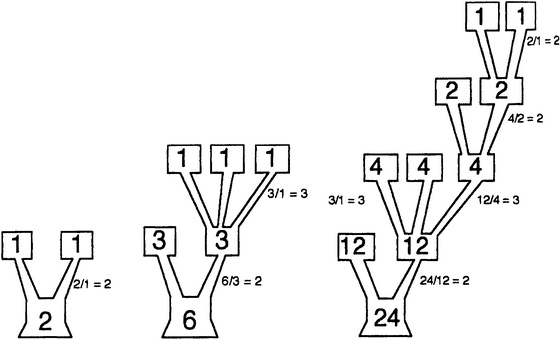

Теперь мы начинаем видеть красоту идеи Галуа. Из нее следует не только доказательство неразрешимости общего уравнения пятой степени в радикалах, но и объяснение, почему общие уравнения второй, третьей и четвертой степени все же имеют решения в радикалах; более того, примерно видно то, и как эти решения устроены. Если поработать еще немного, можно извлечь и точный вид этих решений. Наконец, подход Галуа позволяет отличить те уравнения пятой степени, которые нельзя решить, от тех, которые можно, и говорит нам, как решить эти последние.

Группа Галуа всякого уравнения сообщает нам все, что мы можем пожелать узнать о его решениях. Так почему же Пуассон, Коши, Лакруа и все остальные специалисты не запрыгали от радости, увидев, что же сделал Галуа?

Группа Галуа хранит ужасную тайну.

Тайна эта такого рода. Самый простой способ получить группу какого-либо уравнения состоит в использовании свойств его корней. Но, разумеется, все дело как раз в том, что мы, как правило, не знаем, каковы эти корни. Не будем забывать, что цель состоит в решении уравнения, то есть в нахождении его корней.

Предположим, что кто-то подарит нам конкретное уравнение пятой степени, скажем

или

и попросит использовать методы Галуа, чтобы определить, можно ли решить его в радикалах. Вполне законный вопрос.

Страшная правда состоит в том, что с использованием методов, доступных Галуа, нет никакого способа на него ответить. Можно утверждать, что скорее всего соответствующая группа содержит все 120 перестановок — и если это так, то тогда решить уравнение нельзя. Но мы не знаем наверняка, действительно ли появляются все 120 перестановок. Быть может, пять корней удовлетворяют некоторому специальному условию. Откуда нам знать?

Сколь бы красивой ни была теория Галуа, ей присущи жесткие ограничения. Она имеет дело не с коэффициентами, а с корнями. Другими словами — не с тем, что известно, а с тем, что неизвестно.

Сегодня можно зайти на подходящий математический веб-сайт, ввести туда свое уравнение, и сайт вычислит для вас его группу Галуа. Сегодня известно, что первое из приведенных выше уравнений не разрешимо в радикалах, а второе разрешимо. Я хочу подчеркнуть здесь не то, что мы используем компьютер, а тот факт, что кто-то выяснил, какие шаги надо предпринять для решения задачи. Главнейшее после Галуа продвижение в этой области состояло в разработке способов вычисления группы Галуа любого заданного уравнения.

У самого Галуа таких методов не было. Предстояло пройти целому столетию, чтобы рутинные вычисления групп Галуа стали возможны. Отсутствие же таких методов частично оправдывает реакцию Коши и Пуассона. Они могли сетовать, причем с полным основанием, что идеи Галуа не позволяли решить проблему о разрешимости в радикалах любого данного уравнения.

Чего они не смогли увидеть, так это того факта, что метод Галуа на самом деле решал чуть другую задачу: определить, какие свойства корней делают уравнение разрешимым. Эта задача получила изящный и глубокий ответ. Что же касается задачи, решение которой они хотели бы получить от Галуа… ну, в ней нет причин ожидать четкого ответа. Просто не существует ясного способа классифицировать разрешимые уравнения в терминах легковычисляемых свойств их коэффициентов.

До сих пор интерпретация групп как симметрий несколько отдавала метафорой. Теперь нам надо сделать ее более буквальной, и этот шаг потребует более геометрической точки зрения. Последователи Галуа быстро осознали, что соотношение между группой и симметрией намного легче понять в геометрическом контексте. На самом деле именно так этот предмет обычно и объясняют в учебных курсах.