Наша математическая вселенная. В поисках фундаментальной природы реальности - читать онлайн книгу. Автор: Макс Тегмарк cтр.№ 101

Выше мы рассмотрели тесную взаимосвязь математических структур с вычислениями, при которой первые определяются вторыми. С другой стороны, вычисления — не более чем частный случай математических структур. Так, информационное содержание (состояние памяти) цифрового компьютера — эта строка битов (скажем, 1 001 011 100 111 001…) большой, но конечной длины, эквивалентная некоему большому, но конечному целому числу n, записанному в двоичной системе. Обработка информации в компьютере — это детерминистическое правило изменения каждого состояния памяти на другое (применяемое снова и снова). Так что математически это просто отображающая целые числа на себя функция f, которая многократно применяется: n f(n) f(f(n)) … Иными словами, даже самая сложная компьютерная модель — это не более чем частный случай математической структуры, а значит, она включается в мультиверс IV уровня.

На рис. 12.6 показано, как вычисления и математические структуры связаны не только друг с другом, но также с формальными системами — абстрактными символическими системами аксиом и правил вывода, которые математики применяют для доказательства теорем о математических структурах. Прямоугольники на рис. 12.1 соответствуют таким формальным системам. Если формальная система описывает математическую структуру, то говорят, что последняя является моделью первой. Более того, вычисления могут порождать теоремы в формальных системах (для некоторых классов формальных систем существуют алгоритмы, способные вычислить все теоремы).

На рис. 12.6 также показано, что во всех трёх вершинах треугольника потенциально существуют проблемы: отношения в математических структурах могут быть неопределёнными, формальные системы могут содержать неразрешимые утверждения, а вычисления могут не останавливаться после конечного количества шагов. Отношения между тремя вершинами и соответствующими трудностями обозначены шестью стрелками, смысл которых я подробно объяснил в статье 2007 года о математической Вселенной. Поскольку разные стрелки изучаются специалистами из разных областей — от математической логики до информатики, — исследование этого треугольника как целого является междисциплинарным. Я думаю, оно заслуживает большего внимания.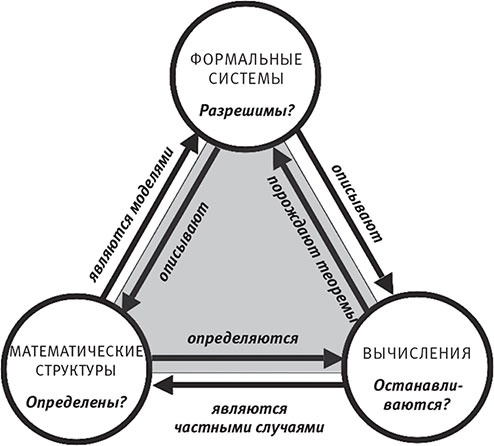

Рис. 12.6. Стрелки обозначают тесные взаимосвязи между математическими структурами, формальными системами и вычислениями. Вопросительный знак указывает на то, что всё это аспекты одной трансцендентной структуры, природу которой мы до конца пока не понимаем.

В центре треугольника я поставил вопросительный знак. Он указывает на предположение, что три вершины (математические структуры, формальные системы и вычисления) являются просто аспектами одной лежащей в основе трансцендентной структуры, природу которой мы пока понимаем не до конца. Эта структура — возможно, ограниченная до определённой (разрешимой, останавливающейся) части, как в ГВВ, существует где-то в свободном от «багажа» виде и являет собой всю полноту математического и физического существования.

В этой главе мы смогли показать, что фундаментальная физическая реальность является мультиверсом IV уровня, и начали разбирать его математические свойства. Теперь займёмся его физическими свойствами, а также следствиями, вытекающими из самой идеи мультиверса IV уровня.

Симметрии и не только

Если взять конкретную математическую структуру из нашего списка, служащего атласом мультиверса IV уровня, то как вывести физические свойства, которые будут восприниматься находящимся в ней самосознающим наблюдателем? Иными словами, каким образом бесконечно разумный математик, начав с математического определения структуры, выводит физические свойства, которые мы в гл. 9 назвали «консенсусной реальностью»? ^[85]

В гл. 10 мы показали, что его первым шагом стало бы вычисление того, какими симметриями обладает математическая структура. Свойства симметрии относятся к числу тех немногих типов свойств, которыми обладает любая математическая структура, и они могут для обитателей данной структуры проявляться как физические симметрии.

По большому счёту, вопрос о том, что именно наш математик, исследуя произвольную структуру, должен далее вычислить, неясен. Но меня удивляет, что в конкретной математической структуре, которую мы населяем, дальнейшие исследования её симметрий привели поистине к золотой жиле. Эмми Нётер в 1915 году доказала, что каждая непрерывная симметрия нашей математической структуры приводит к так называемому закону сохранения в физике, то есть к тому, что некоторая величина гарантированно остаётся неизменной и возникает постоянство, которое может быть замечено самосознающими наблюдателями и получить у них «багажное» название. Все сохраняющиеся величины, которые мы обсуждали в гл. 7, соответствуют таким симметриям. Например, энергия соответствует симметрии относительно переноса во времени (то есть тому, что законы физики остаются всегда одинаковыми), импульс соответствует симметрии переноса в пространстве (тому, что законы остаются одинаковыми везде), угловой момент соответствует вращательной симметрии (тому, что пустое пространство не имеет выделенного направления «верх»), а электрический заряд соответствует определённой симметрии в квантовой механике. Венгерский физик Юджин Вигнер обнаружил, что эти симметрии также диктуют все квантовые свойства, которыми могут обладать частицы, включая массу и спин. Иными словами, Нётер и Вигнер показали, что, по крайней мере в нашей математической структуре, изучение симметрий открывает, какого рода «материи» могут в ней существовать. Как говорилось в главе 7, некоторые мои коллеги любят в шутку сказать, что частица — это просто «элемент неприводимого представления группы симметрии». Становится ясно, что почти все наши физические законы вытекают из симметрий, а лауреат Нобелевской премии по физике Филип Уоррен Андерсон пошёл ещё дальше, заявив, что «лишь небольшое преувеличение сказать, что физика сводится к изучению симметрии».

Почему симметрии играют такую важную роль в физике? ГМВ отвечает, что физическая реальность обладает свойствами симметрии, поскольку она математическая структура, а математические структуры обладают свойствами симметрии. Тогда более глубокий вопрос о том, почему конкретная структура, в которой мы обитаем, имеет так много симметрий, становится эквивалентным вопросу о том, почему мы оказались в этой конкретной структуре, а не в другой, обладающей меньшей симметрией. Ответ может состоять отчасти в том, что симметрии, по-видимому, скорее правило, чем исключение для математических структур — особенно крупных, находящихся не очень далеко внизу в основном списке (то есть таких, для которых простые алгоритмы определяют отношения большого числа элементов, из-за чего у всех них много общих свойств). Также может сказываться эффект антропной селекции: как отмечал Вигнер, существование наблюдателей, способных замечать закономерности в окружающем их мире, вероятно, требует симметрий, так что, раз мы являемся наблюдателями, следует ожидать, что мы окажемся в высокосимметричной математической структуре. Представьте себе попытку понять мир, в котором эксперименты никогда не повторяются, поскольку их исход зависит от того, где и когда вы их выполняете. Если бы брошенный камень иногда падал вниз, иногда летел вверх, да и всё остальное вело бы себя внешне произвольным образом, не было бы смысла в развитии мозга.