
|
||
|
|
Онлайн книга - Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике | Автор книги - Джон Дербишир
Cтраница 99

Среди упомянутых средств обращения имеется еще один метод, который позволяет вывернуть полученное выражение наизнанку и записать J через ζ. Я немного потяну с предъявлением обращенного выражения. Но логика во всяком случае ясна: • можно выразить π(x) через J(x) (раздел IV данной главы); • обратив выражение (19.6), можно выразить J(x) через дзета-функцию и, следовательно, • можно выразить π(x) через дзета-функцию. Именно за это предприятие Риман и взялся, потому что в результате окажется, что все свойства функции π некоторым образом закодированы в свойствах ζ-функции. Функция π относится к теории чисел; ζ-функция относится к анализу, и мы перебросили понтонный мост через пролив, разделяющий два берега — счет и измерение. Коротко говоря, мы только что получили мощный результат в аналитической теории чисел. На рисунке 19.6 графически представлено выражение (19.6) — Золотой Ключ в аналитическом виде. 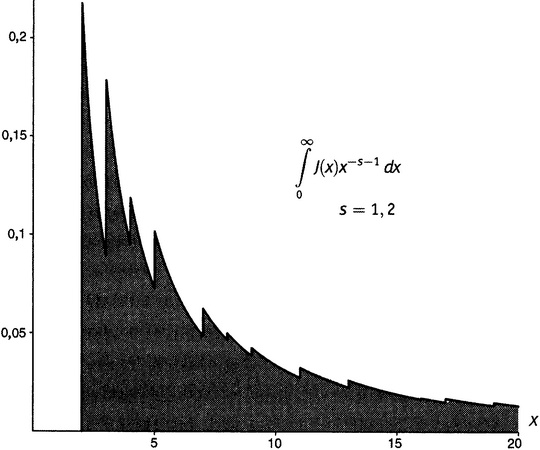
Рисунок 19.6. Затемненная область представляет собой интеграл
Глава 20. Риманов оператор и другие подходы
I. Закон Монтгомери-Одлыжко утверждает, что нетривиальные нули дзета-функции Римана выглядят — имеется в виду статистически — как собственные значения некоторой случайной эрмитовой матрицы. Операторы, представляемые такими матрицами, можно использовать для моделирования определенных динамических систем в квантовой физике. А имеется ли при этом оператор Римана — оператор, собственные значения которого в точности совпадают с нулями дзета-функции? Если да, то какую динамическую систему он представляет? Удастся ли создать такую систему в физической лаборатории? И если удастся, то поможет ли это в доказательстве Гипотезы? Эти вопросы активно изучались еще до выхода статьи Одлыжко 1987 года. За год до того Майкл Берри опубликовал статью под заглавием «Дзета-функция Римана: Модель квантового хаоса?». Используя ряд хорошо известных и широко обсуждавшихся в то время результатов (и среди них некоторые результаты Одлыжко), Берри обратился к следующему вопросу. Предположим, что риманов оператор существует; тогда динамическую систему какого типа он бы моделировал? Ответ, который он предложил, — хаотическую систему. Чтобы объяснить это, нам надо ненадолго переключиться на знакомство с теорией хаоса. II. Тот факт, что чистая теория чисел — наука о натуральных числах и их взаимоотношениях — может соотноситься с субатомной физикой, вовсе не удивителен. В квантовой физике арифметическая составляющая выражена намного сильнее, чем в классической физике, поскольку основополагающая идея состоит в том, что материю и энергию нельзя делить до бесконечности. Энергия передается только в виде 1, 2, 3 или 4 квантов, но никак не 11/2, 217/52, √2 или π квантов. Это, конечно, далеко не все, что есть в квантовой механике; ее саму невозможно было бы разработать без наиболее мощных средств самого современного анализа. Например, знаменитое волновое уравнение Шредингера записывается на традиционном языке дифференциального исчисления. Тем не менее арифметическая составляющая в квантовой механике несомненно присутствует, тогда как в классической механике ее практически вовсе нет. Основания классической физики — физики Ньютона и Эйнштейна — по сути своей аналитические, в математическом смысле. Они опираются на математический анализ, на понятия бесконечной делимости, гладкости и непрерывности, предела и производной, а также вещественных чисел. Не будем забывать, что, именно развивая и доводя понятие «предела» до логического конца, Ньютон и изобрел дифференциальное и интегральное исчисление, в конце концов ставшее содержанием большей части анализа. Рассмотрим классическую задачу о движении одного тела вокруг другого по эллиптической орбите под действием силы их взаимного гравитационного притяжения. На некотором расстоянии (измеряемом вещественным числом r) от основного тела другое тело (спутник) имеет некоторую строго определенную скорость (выражаемую другим вещественным числом v). Связь между v и r дается точным математическим выражением; v есть в действительности функция от r, выражаемая так называемым уравнением vis viva [179], знакомым всем, кто изучал элементарную небесную механику: 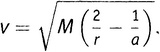
где M и a — некоторые заданные числа, определяемые параметрами системы и начальными условиями — в частности, массами тел и т.п. На практике, конечно, нельзя достичь бесконечной точности, требуемой для того, чтобы присвоить определенные вещественные значения величинам r и v. Пусть даже мы измеряем r с точностью до 10 или даже 20 знаков после запятой; но ведь для точного выражения вещественного числа требуется бесконечно много десятичных разрядов, а добиться такого мы не можем. Следовательно, для любой реальной орбиты имеется некоторая, пусть очень малая, ошибка при определении вещественных значений буквы r, а также соответствующая ошибка в вычисленных значениях буквы v. Это не играет большой роли: законы Кеплера уверяют нас, что все равно получится правильный эллипс, а математика уравнения vis viva говорит, что ошибка в 1 процент при определении r, как правило, приведет лишь к 0,5-процентной ошибке при вычислении значений v. Таким образом, ситуация управляема и предсказуема. Как говорят математики, «задача интегрируема». Но это была очень простая задача. Почти все реальные физические проблемы сложнее, чем эта. Рассмотрим, например, случай трех тел, испытывающих взаимное гравитационное притяжение, — знаменитую «задачу трех тел». Можно ли найти ее решение в замкнутом виде, как для уравнения vis viva? Интегрируема ли она?
|
|
|||||||||||||||||||||||||||||||||||||||||||||
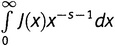 при s = 1,2. Его численное значение составляет 1,434385276163. Он равен 1/s∙ln ζ(s).
при s = 1,2. Его численное значение составляет 1,434385276163. Он равен 1/s∙ln ζ(s). Вернуться к просмотру книги
Вернуться к просмотру книги
 Перейти к Оглавлению
Перейти к Оглавлению
 Перейти к Примечанию
Перейти к Примечанию
 © 2020 LoveRead.ec - электронная библиотека в которой можно
© 2020 LoveRead.ec - электронная библиотека в которой можно