Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике - читать онлайн книгу. Автор: Джон Дербишир cтр.№ 92

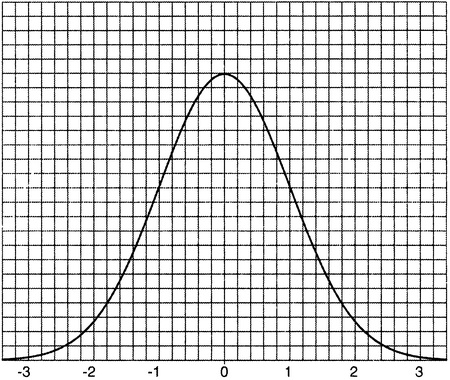
Представим себе стандартную колоколообразную кривую, нарисованную на разлинованном листе бумаги с очень мелкими делениями, так что под кривой расположены сотни квадратиков, образованных разметкой листа (рис. 18.1). Случайным образом выберем один из этих квадратиков; расстояние по горизонтали от него до вертикальной линии, проходящей через середину пика, представляет собой случайное число с нормальным гауссовым распределением. Вблизи самого пика скопилось намного больше этих квадратиков, чем под хвостами кривой, так что с гораздо более высокой вероятностью мы выберем число между +1 и −1, нежели число справа от +2 или слева от −2. Это же видно и из приведенной выше матрицы. (Впрочем, по некоторым техническим причинам элементы на ее главной диагонали в действительности представляют собой случайные гауссовские числа, умноженные на √2, а потому их значения — несколько большие, чем того следовало ожидать.)

Оказалось, что случайные гауссовы эрмитовы матрицы — только гораздо, гораздо большего размера — позволяют моделировать поведение определенных квантовых динамических систем. В частности, их собственные значения, как выяснилось, прекрасно соответствуют энергетическим уровням, которые наблюдаются в экспериментах. По этой причине в 1960-х годах эти собственные значения — собственные значения случайных эрмитовых матриц — стали объектом пристального изучения. В частности, очень интересными оказались интервалы между собственными значениями. Эти интервалы не распределены случайным образом. Например, два уровня оказываются близко друг к другу с гораздо меньшей вероятностью, чем можно было бы ожидать, исходя из случайного распределения. Это явление получило название «отталкивания» — энергетические уровни стараются разойтись по возможности дальше друг от друга, как длинная очередь из малосимпатичных друг другу людей.

Чтобы сделать некое наглядное пособие по этой теме, я попросил математическую программу Mathematica 4, которой я пользуюсь, создать случайную эрмитову матрицу размером 269×269 и вычислить ее собственные значения (рис. 18.2). Причина, по которой выбрано число 269, станет ясной очень скоро. Mathematica, которая не перестает меня удивлять, справилась с задачей в мгновение ока. Все 269 собственных значений попали в интервал от −46,207887 до 46,3253478. Моя идея заключалась в том, чтобы нанизать их, как бусинки, на прямую, тянущуюся от −50 до +50, чтобы они висели там, как дождевые капли на проволочной ограде, а мы, глядя на них, смогли увидеть, имеется ли какой-нибудь порядок в распределении интервалов между ними. Однако это оказалось неосуществимым в пределах книжной страницы, поэтому пришлось порезать прямую на десять отрезков (от −50 до −40, от −40 до −30 и т.д.) и поместить эти отрезки один над другим. В результате получился рисунок 18.2.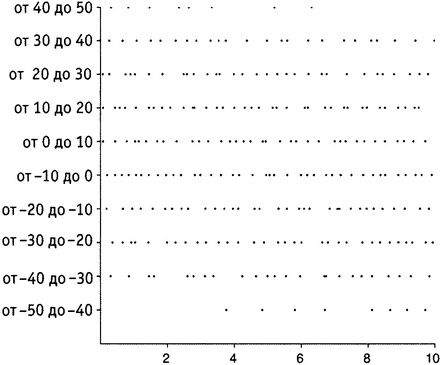

Никакого явного закона в распределении интервалов не просматривается. Хочется сказать, что они случайны. Но нет! На рисунке 18.3 показаны 269 чисел, выбранных совершенно случайно в интервале от 0 до 10 и изображенных тем же образом. Сравнение рисунков 18.2 и 18.3 позволяет увидеть, что собственные значения случайной матрицы раскиданы по прямой не случайным образом. На рисунке 18.2 заметен эффект отталкивания, тогда как для случайного разброса на рисунке 18.3 мы видим, что имеется большее по сравнению с распределением собственных значений число пар, расположенных достаточно близко друг к другу (а потому, неизбежно, и большее количество тех, что сидят дальше друг от друга). Хотя собственные значения на рисунке 18.2 и отказываются следовать какому-нибудь заметному глазу порядку (в конце концов, они же возникли из случайной матрицы!), они все же изо всех сил стараются сохранять дистанцию между собой. Напротив, чисто случайная точка, судя по всему, совсем не возражает, если ее прижмут к другой случайной точке.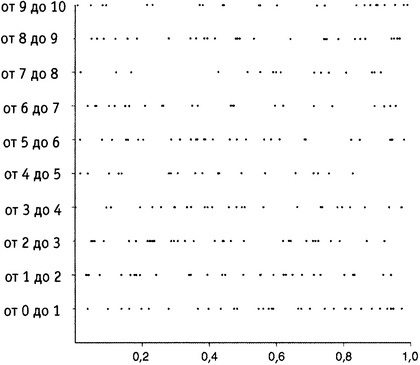

Позвольте ввести три профессиональных термина, имеющие прямое отношение к обсуждаемому вопросу. Множество случайных (т.е. гауссовых случайных) эрмитовых матриц ^[164]{A9} описанного типа называется во всей своей совокупности «гауссовым унитарным ансамблем» (ГУА). Точные статистические свойства интервалов в длинных неоднородных строках из чисел типа тех, что фигурируют в приведенных примерах, выражаются так называемой парной корреляционной функцией. А некоторое отношение, связанное с этой функцией и достаточно точно эту функцию характеризующее, называется формфактором.

Теперь я готов рассказать о знаменательной встрече, которая привела к постановке весьма странных и загадочных вопросов о Гипотезе Римана и впоследствии послужила «виновницей» тысяч исследовательских проектов.

III.

Эта встреча произошла в 1972 году, когда в Институте высших исследований в Принстоне случайно столкнулись специалист по теории чисел и физик. Специалистом по теории чисел был Хью Монтгомери — молодой американец, который тогда состоял в аспирантуре в кембриджском Тринити-колледже — колледже Г.X. Харди. Физиком же был Фримен Дайсон, который в то время являлся профессором в принстонском Институте высших исследований. Дайсон, которого мы уже упоминали, был известным физиком. В тот момент он еще не освоил параллельную профессию автора наводящих на размышления бестселлеров о происхождении и будущем человеческого рода.

Как раз незадолго до этого Хью Монтгомери исследовал интервалы между нетривиальными нулями дзета-функции. Это исследование не было частью программы по возможному доказательству Гипотезы Римана. Просто так случилось, что определенный результат о природе этих интервалов имел приложения в области теории чисел, для полей, несколько напоминающих поле а + b√2, с которым мы познакомились в главе 17.ii. ^[165] Этим и занимался Монтгомери. Вот как звучит эта история в его собственном изложении: