
|
||
|
|
||
|
|
Онлайн книга - Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике | Автор книги - Джон Дербишир
Cтраница 88

III. Краткий взгляд на размах, мощь и красоту теории алгебраических полей — это все, на что нам здесь хватает места, хотя мы и вернемся ненадолго к полям, рассмотрев их под другим углом зрения в главе 20.v. Я привел здесь этот краткий обзор алгебраических сведений, потому что в 1921 году Артин в своей диссертации, которую он защищал в Лейпцигском университете, применил теорию полей для развития нового подхода к Гипотезе Римана. Соответствующий математический аппарат достаточно серьезен, и я расскажу о нем лишь очень бегло. Как уже упоминалось в предыдущем разделе, для всякой степени pN простого числа имеется конечное поле. Мы также видели, как конечное поле можно использовать в качестве основы для построения других полей, в том числе бесконечных. Оказывается, что если начать с конечного поля, то имеется способ таким образом построить эти поля-«расширения», что с ними будет связана некоторая дзета-функция. Под «некоторой дзета-функцией» здесь понимается функция комплексного аргумента, определенная над полем комплексных чисел и по целому ряду своих свойств необъяснимым образом напоминающая дзета-функцию Римана. Например, эти аналоги римановой дзета-функции снабжены своим собственным Золотым Ключом — своей собственной эйлеровой формулой произведения, а также своей собственной Гипотезой Римана. [160] В 1933 году работавшему в Магдебургском университете в Германии Хельмуту Хассе удалось для определенной категории полей доказать результат, аналогичный Гипотезе Римана. В 1942 году Андре Вейль [161] распространил это доказательство на гораздо более широкий класс объектов, а затем предположил — в знаменитых трех «гипотезах Вейля», — что подобные результаты должны иметь место для еще более широкого класса. В 1973 году бельгийский математик Пьер Делинь получил сенсационное достижение, принесшее ему Филдсовскую премию, — он доказал гипотезы Вейля, тем самым, по существу, завершив программу исследований, начало которой положил Артин. Неизвестно, в какой степени методы, развитые для доказательства аналогов Гипотезы Римана, относящихся к столь замысловатым полям, пригодны для доказательства классической Гипотезы Римана. Но очень многие считают, что вполне пригодны, и данная область остается очень активным направлением в исследовании Гипотезы Римана. Ведут ли эти исследования куда-нибудь? Это не ясно — по крайней мере, мне не ясно. По поводу существа дела обратимся снова ко второму абзацу в этом разделе, где говорилось, что с полями определенного вида связаны аналоги дзета-функции. Для классической дзета-функции — той, о которой говорится в исходной Гипотезе Римана и которой главным образом и посвящена данная книга, — полем такого вида будет Q, поле обычных рациональных чисел. По мере развития исследований в последние десятилетия выяснилось, что элементарное поле рациональных чисел Q в некотором смысле глубже и более своенравно, нежели «искусственно выведенные» поля, к которым применимы результаты Артина, Вейля и Делиня. Но с другой стороны, методы, развитые для обращения с этими «искусственными» полями, оказались достаточно мощными — Эндрю Уайлс использовал их для доказательства Последней теоремы Ферма! IV. Для понимания физической линии в исследовании Гипотезы Римана, генезис которой будет описан в разделе VI и которая открыла исследователям новые обширные территории, следует обратиться к другой алгебраической теме — теории операторов. Поэтому данный раздел, как и следующий, посвящен рассказу об операторах, рассматриваемых с точки зрения связанной с ними теории матриц. В современной математике и физике матрицы вездесущи, и способность управляться с ними относится к числу основных математических навыков. Из-за ограничений в объеме мне придется спрямить историю, приведя лишь самое необходимое. В частности, я вообще обойду стороной вопрос о вырожденных матрицах, как если бы таких в природе не было. Это, должно быть, самое возмутительное упрощение во всей книге, и я приношу свои извинения математически подкованным читателям. Матрица — это квадратная таблица из чисел, например
Если даны две матрицы одного и того же размера, то их можно складывать, вычитать, умножать и делить. Правила, по которым выполняются эти действия, не сразу очевидны. Например, если A и B — две матрицы одного и того же размера, то, вообще говоря, не верно, что А×В = В×А. Правила обращения с матрицами несложно найти в любом обычном учебнике по алгебре, и нам нет нужды вдаваться в них. Достаточно сказать, что такие правила существуют и что имеется арифметика матриц, в целом напоминающая арифметику обычных чисел, только похитрее. Нам же важно знать про матрицы следующее. Из всякой матрицы (N×N) можно извлечь многочлен N-й степени — полиномиальную функцию, составленную из различных степеней буквы x, вплоть до N-й степени. Боюсь, я не могу объяснить, как же найти этот многочлен для данной матрицы. Придется поверить мне, что он действительно существует и что имеется способ его построить. Этот многочлен называется характеристическим многочленом матрицы. Характеристический многочлен для приведенной выше матрицы 2×2 равен x2 − 11x + 28. [162] При каких значениях x этот многочлен равен нулю? Это все равно что спросить, каковы решения квадратного уравнения x2 − 11x + 28. По хорошо известной формуле (или, как оптимистически говаривал мой школьный учитель, «путем усмотрения») находим, что решения — это 4 и 7. Ну и правда, если подставить 4 вместо x, то значением многочлена будет 16 − 44 + 28, что в самом деле равно нулю. То же самое и с подстановкой числа 7: 49 − 77 + 28 тоже равно нулю.
|
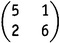 . Целые числа выбраны здесь исключительно для простоты. Числа, входящие в матрицу, могут быть рациональными, вещественными или даже комплексными. Данная конкретная матрица — это матрица 2×2. Матрицы могут быть любого размера, скажем, 3×3, 4×4, 120×120 и т.д. Они могут иметь даже бесконечный размер, хотя для бесконечных матриц правила и подвергаются некоторой модификации. Важная часть во всякой матрице — это ее главная диагональ, т.е. диагональ, ведущая из левого верхнего угла в правый нижний. В нашем примере на главной диагонали стоят элементы 5 и 6.
. Целые числа выбраны здесь исключительно для простоты. Числа, входящие в матрицу, могут быть рациональными, вещественными или даже комплексными. Данная конкретная матрица — это матрица 2×2. Матрицы могут быть любого размера, скажем, 3×3, 4×4, 120×120 и т.д. Они могут иметь даже бесконечный размер, хотя для бесконечных матриц правила и подвергаются некоторой модификации. Важная часть во всякой матрице — это ее главная диагональ, т.е. диагональ, ведущая из левого верхнего угла в правый нижний. В нашем примере на главной диагонали стоят элементы 5 и 6. Вернуться к просмотру книги
Вернуться к просмотру книги
 Перейти к Оглавлению
Перейти к Оглавлению
 Перейти к Примечанию
Перейти к Примечанию
 © 2020 LoveRead.ec - электронная библиотека в которой можно
© 2020 LoveRead.ec - электронная библиотека в которой можно