Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике - читать онлайн книгу. Автор: Джон Дербишир cтр.№ 77

Cтраница 77

Этим иллюстрируется и еще один аспект Ο большого. Ο большое игнорирует не только знаки, но и множители. Если A есть Ο большое от B, то таковыми же будут 10A, 100A и 1000 000A; таковыми будут и одна десятая A одна сотая A одна миллионная A. Ο большое не сообщает нам о точном темпе роста — для этого у нас есть производные. Она сообщает о типе роста. Функция «единица» вообще не имеет никакого темпа роста — она намертво постоянная. Функция, являющаяся Ο большим от единицы, никогда не возрастет быстрее этого. Она может выделывать всякое другое: прижиматься к нулю, колебаться без конца внутри ограничивающих ее прямых или же подходить к одной из ограничительных линий все ближе и ближе, но она никогда не взовьется внезапно вверх и не нырнет внезапно вниз, прорываясь через эти линии и оставаясь после этого снаружи.

Приведенные функции 0,1x, 0,01x, 0,001x и 0,0001x — не Ο большое от единицы; все они — Ο большое от x. Такова же и любая другая функция, которая остается навсегда заключенной в «куске пиццы» между прямой ax и ее зеркальным отражением −ax. На рисунке 15.2 приведен пример функции, которая не остается в таких пределах. Это 0,1x² — квадратичная функция. Не важно, сколь широким вы сделаете этот кусок пиццы — т.е. не важно, сколь велико значение a, — график функции 0,1x² рано или поздно прорвется через верхнюю границу.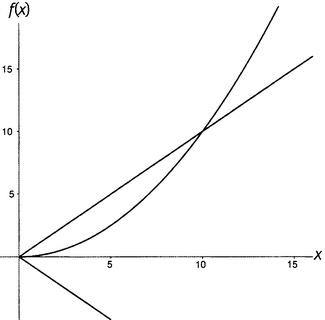

Теперь мы можем оценить значение результата фон Коха 1901 года. Если Гипотеза Римана верна, то при x, стремящемся к бесконечности, абсолютная разность между π(x) и Li(x) — т.е. или Li(x) − π(x), или π(x) − Li(x), что не важно, потому что Ο большому нет дела до знаков, — остается заключенной между двумя ограничивающими кривыми. Ограничивающие кривые — это C√x∙ln x и ее зеркальное отражение, где C — некоторое число. Остаточный член может делать что хочет между этими двумя кривыми, но он никогда не выберется наружу и никогда не вырвется внезапно из-под их контроля. Разность между π(x) и Li(x) есть Ο большое от √x∙ln x.

На рисунке 15.3 приведен пример функции, которая есть Ο(√x∙ln x). Там показаны: 1) кривая √x∙ln x (верхняя половина отдаленно напоминающей параболу кривой), 2) зеркально отраженная кривая −√x∙ln x (нижняя половина) и 3) придуманная для иллюстрации и ничего особенно не выражающая функция, которая есть Ο(√x∙ln x). Буква m обозначает миллион, ведь вещи подобного рода интересны только для больших аргументов. Стоит отметить, что "функция Дербишира" в действительности на некоторое время вырывается за пределы ограничивающих ее кривых при аргументах, равных примерно 200 миллионам. Это не страшно, поскольку больше она никогда такого не делает. Начиная с некоторой точки — и навсегда после нее — функция остается в пределах границ. Верьте мне, что она там остается, хотя по понятным причинам я и не могу показать вам всю функцию до бесконечности. Ο большое принимает во внимание исключения из правил при малых аргументах (а такие исключения — общее место в теории чисел, взять хотя бы утверждение «все простые числа нечетные… кроме самого первого»).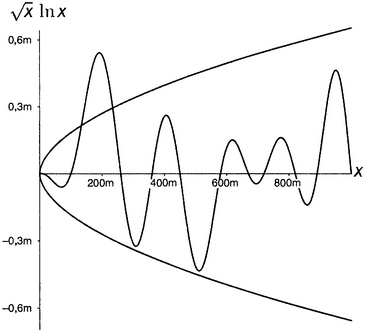

Можно заметить еще, что, поскольку Ο большое не принимает во внимание множители, масштаб по вертикали совершенно произволен. Важны лишь конфигурация — форма ограничивающих кривых — и тот факт, что начиная с какого-то места наша функция навсегда заключена между ними.

III.

Результат фон Коха 1901 года ^[135] — а именно утверждение, что, если Гипотеза Римана верна, то π(x) = Li(x) + Ο(√x∙ln x), — один из первых примеров определенного типа результатов, которыми сейчас полна теория чисел, — результатов, которые начинаются словами «Если Гипотеза Римана верна, то…». Если окажется, что Гипотеза Римана не верна, то немалую часть теории чисел придется переписывать.

А есть ли какой-нибудь результат типа Ο большого для остаточного члена Li(x) − π(x), который не зависел бы от справедливости Гипотезы Римана? О да. Среди специалистов по аналитической теории чисел долгие годы любимым спортом был поиск все лучших и лучших формул типа Ο большого для остаточного члена. Но ни один не может сравниться с Ο(√x∙ln x). Это абсолютно лучшее, наиболее точное ограничение на остаточный член, известное к настоящему моменту. Правда, раз оно зависит от справедливости Гипотезы, мы не можем быть полностью уверены, что оно верно. Все те оценки остаточного члена, в справедливости которых мы уверены, менее точны, чем эта. Соответствующая параболическая кривая на рисунке 15.3 несколько шире, причем различие делается все более заметным по мере того, как x уходит на бесконечность. Если же Гипотеза Римана верна, то среди всех известных оценок остаточного члена выражение Ο(√x∙ln x) является наилучшим возможным — наиболее точной формулой типа Ο большого. Оно же и простейшее. При этом все формулы, которые были доказаны без предположения о справедливости Гипотезы, выглядят достаточно уродливо. Вот наилучшая из тех, что известны мне на данный момент: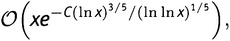

где С — некоторое постоянное число. Ни одна из других подобных формул на вид не проще этой.

Сравним результат фон Коха 1901 года с выделенными курсивом словами в восьмой проблеме Гильберта, приведенной в главе 12.ii. Гильберт перекликался с Риманом, написавшим в своей работе 1859 года, что приближение функции π(x) функцией Li(x) «верно только по порядку величины x^1/2». Ну а √x есть, конечно, попросту x^1/2. Более того, в главе 5.iv мы видели, что ln x растет медленнее, чем любая положительная степень x, даже самая ничтожно малая. Это можно выразить в терминах Ο большого таким образом: для любого сколь угодно малого числа ε выполнено ln x = Ο(x^ε). А следовательно (это, правда, не сразу очевидно, но в действительности несложно доказать), можно подставить x^ε вместо ln x в выражение Ο(√x∙ln x); а поскольку √x — это просто x^1/2, можно сложить степени и получить Ο(x^1/2+ε). Таким путем получается довольно распространенный вид результата фон Коха: π(x) = Li(x) + Ο(x^1/2+ε). Символ ε настолько часто используется для исчезающе малых чисел, что слова «… для любого сколь угодно малого ε» здесь подразумеваются.