Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике - читать онлайн книгу. Автор: Джон Дербишир cтр.№ 70

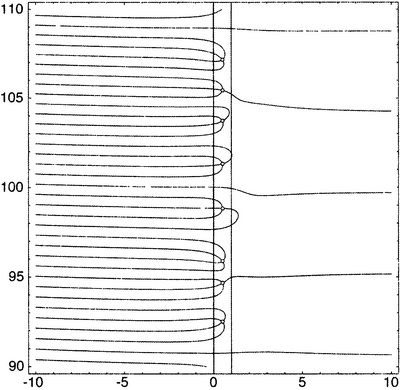
Ha самом деле имеется правило, позволяющее найти средний интервал между нулями на высоте T в критической полосе. Этот интервал ~ 2π/ln (T/2π). Если T равно 20, то это выражение вычисляется как 5,4265725…. Если T равно 100, то оно равно 2,270516724…. Как можно видеть, правило не слишком точное, хотя знак волны говорит нам, что оно становится все точнее по мере того, как числа растут. Эндрю Одлыжко опубликовал список 10 000 нулей в окрестности числа ¹/₂ + 1370919909931995308897i. Там за 2π/ln (T/2π) дают что-то около 0,13516467, а среднее, вычисленное для 9999 интервалов, равно 0,13417894…. Не так плохо!

Остановимся на еще одном моменте, который окажется довольно важным в дальнейшем изложении. Имеется симметрия относительно вещественной (т.е. идущей с запада на восток) оси. Если продлить рисунок 13.6 на юг от вещественной оси, линии окажутся зеркальными отображениями линий из северной половины. Единственная разница состоит в том, что если вещественные числа, отмеченные на рисунке 13.6, будут одинаковыми на юге и на севере, то мнимые числа поменяют знак. Математически это выражается так, что если ζ(a + bi) = u + vi, то ζ(a − bi) = u − vi. Или, если по-настоящему использовать язык комплексных чисел, ζ(z') = ζ'(z). Важное следствие отсюда состоит в том, что если a + bi — нуль дзета-функции, то a − bi — тоже нуль.

IX.

И наконец, графическое представление Гипотезы Римана — или по крайней мере того факта, что на критической прямой полно нулей.

Чтобы разобраться в рисунке 13.8, вспомним, что рисунки 13.6 и 13.7 изображают плоскость аргумента. Функция комплексной переменной отправляет комплексные числа из одного множества (аргументы) в другое множество (значения). Поскольку комплексные числа располагаются на плоскости, можно представлять себе, что функция отправляет точки из одной плоскости (плоскости аргумента) в точки на другой плоскости (плоскости значений). Дзета-функция отправляет точку ¹/₂ + 14,134725i на плоскости аргумента в точку 0 на плоскости значений. Взглянем снова на рисунок 13.2. Там плоскость аргумента и плоскость значений показаны одновременно — как если бы это были наложенные друг на друга прозрачные пленки для проектора.

Рисунки 13.6 и 13.7 изображают плоскость аргумента; там указано, какие аргументы отправляются в интересные нам значения. Муравей Арг живет на плоскости аргумента — потому его так и назвали. Он бродит по этой плоскости, отмечая, какие точки отправляются в нули при применении дзета-функции. Он у нас путешествовал по странным кривым и завиткам, образованным точками, которые отправляются в чисто вещественные или чисто мнимые числа (т.е. точками, в которых дзета-функция имеет чисто вещественные или чисто мнимые значения). Будем говорить, что это — изображения плоскости аргумента типа «отсюда», имея в виду, что отсюда дзета-функция отображает во что-то интересное.

Альтернативным способом функцию можно представить, показав картинку типа «сюда» на плоскости значений. ^[115] Вместо того чтобы показывать, как это делалось на рисунках 13.6 и 13.7, какие аргументы отправляются в интересные нам значения (а такими у нас были чисто вещественные и чисто мнимые числа), можно дать картину плоскости значений, на которой будет показано, в какие значения отображаются интересующие нас аргументы.

Представим себе, что у муравья Арга есть брат-близнец, который живет на плоскости значений.^{A4} Зовут его, понятно, муравей Знач. И допустим еще, что близнецы постоянно общаются между собой по рации и таким способом синхронизируют свои передвижения, так что, на каком бы аргументе ни находился муравей Арг в любой момент времени, муравей Знач стоит на соответствующем значении в плоскости значений. Если, например, муравей Арг стоит на числе ¹/₂ + 14,134725i, а на его приборчике выставлена дзета-функция, то муравей Знач стоит на числе 0 в своей плоскости (плоскости значений).

Предположим теперь, что муравей Арг, вместо того чтобы ползать по всем этим причудливым завитушкам, изображенным на рисунке 13.6 (что заставляет муравья Знача скучать, вышагивая взад и вперед по вещественной и мнимой осям), предпримет прогулку прямо по критической прямой, направляясь на север из аргумента ¹/₂. По какой траектории будет тогда следовать муравей Знач? Это показано на рисунке 13.8. Его путь начинается в точке ζ(¹/₂), что, как мы видели в главе 9.v, равно −1,4603545088095…. Далее он описывает нечто вроде полуокружности против часовой стрелки ниже нулевой точки, а затем поворачивает и движется по петле по часовой стрелке вокруг точки 1. Он держит путь к нулю и проходит через него (это первый нуль — муравей Арг как раз прошел точку ¹/₂ + 14,134725i). Затем он продолжает описывать петли по часовой стрелке, проходя через нулевую точку снова и снова через некоторый промежуток — всякий раз, как его брат-близнец наступает на нуль дзета-функции на плоскости аргумента. Я прервал путешествие Знача, когда муравей Арг достиг точки ¹/₂ + 35i, потому что рисунок 13.6 продолжается лишь до этих пор. К тому моменту, как эта точка достигнута, кривая на плоскости значений прошла через нуль пять раз, что соответствует пяти нетривиальным нулям на рисунке 13.6. Отметим, что точки на критической прямой демонстрируют выраженную тенденцию к тому, чтобы отображаться в точки с положительной вещественной частью.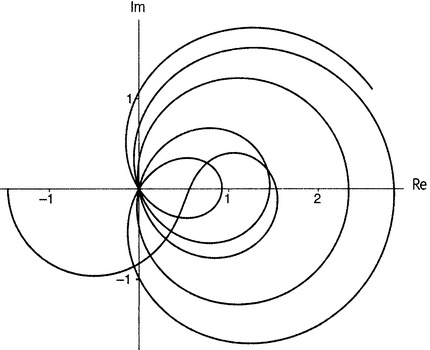

Еще раз: на рисунке 13.8 показана плоскость значении. Это не диаграмма типа «отсюда», подобная рисункам 13.6 и 13.7; наоборот, это диаграмма типа «сюда», которая показывает, что же дзета-функция делает с критической прямой, подобно тому как на рисунке 13.2 было показано, что функция возведения в квадрат делаете расчерченным квадратиком. Если мы желаем выражаться чисто математически, то следует сказать, что завивающаяся в петли кривая на рисунке 13.8 есть ζ(критическая прямая) — множество всех точек, которые происходят из точек на критической прямой. Кривые на рисунках 13.6 и 13.7 суть ζ⁻¹(вещественная и мнимая оси) — множество всех точек, которые дзета-функция отправляет в вещественную и мнимую оси. Мы используем запись «ζ(критическая прямая)», чтобы указать на «все значения дзета-функции при аргументах, лежащих на критической прямой». Наоборот, «ζ⁻¹(вещественная и мнимая оси)» означает «все аргументы, для которых значения дзета-функции лежат на вещественной или мнимой осях». Заметим, что выражение ζ⁻¹ используется здесь в специальном смысле теории функций и указывает на обратную функцию. Не следует путать его с a⁻¹ из 8-го правила действий со степенями, где имеется в виду 1/a, арифметическое обратное числа a. Это другое использование — еще один пример перегрузки математических символов, как и с буквой π, которая обозначает и число 3,14159…, и функцию числа простых чисел.