
|
||
|
|
||
|
|
Онлайн книга - Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике | Автор книги - Джон Дербишир
Cтраница 61

Мне хотелось бы отправиться с вами в обзорное путешествие по 23 проблемам Гильберта. [101] Но тогда эта книга станет недопустимо длинной. А кроме того, имеется обширная, приспособленная к различным уровням понимания литература, с помощью которой такое путешествие осуществимо. [102] Я лишь замечу попутно, что самая первая из проблем Гильберта относилась к упоминавшейся в предыдущей главе континуум-гипотезе, которая посвящена самой сути запутанного вопроса о природе вещественных чисел и возражениям, выдвигавшимся против них Кронеккером. О континуум- гипотезе также имеется обширная литература. Хорошая библиотека или хороший интернет-поисковик вполне удовлетворят любопытство любого, кто захочет обратиться к этой завораживающей задаче. [103] Только одна из проблем Гильберта — восьмая — имеет прямое отношение к теме нашей книги. Вот она — в переводе Мэри Уинстон Ньюсон из Bulletin of the American Mathematical Society [104]: 8. Проблемы простых чисел В теории распределения простых чисел в последнее время сделаны существенные сдвиги Адамаром, Валле Пуссеном, Мангольдтом и другими. Для полного решения проблемы, поставленной в исследовании Римана «О числе простых чисел, не превышающих данной величины», необходимо прежде всего доказать справедливость исключительно важного утверждения Римана: все нули функции ζ(s), определяемой рядом 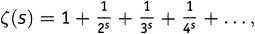
имеют вещественную часть, равную 1/2, если не считать известных отрицательных целочисленных нулей. Как только это доказательство будет получено, то дальнейшая задача будет заключаться в том, чтобы использовать бесконечный ряд Римана для более точного определения числа простых чисел и в особенности выяснить, будет ли разность между числом простых чисел, меньших данного числа x, и интегральным логарифмом от x действительно не выше половинного порядка при неограниченно возрастающем x. Далее, действительно ли те члены формулы Римана, которые зависят от первых комплексных нулей функции ζ(s), обусловливают сгущение простых чисел, которое обнаружено при подсчете числа простых чисел. Тем читателям, которые до сих пор не потеряли нить, этот пассаж должен быть понятен хотя бы отчасти. Я надеюсь, что все целиком приобретет смысл, когда мы доберемся до конца книги. Сейчас главное для нас — тот факт, что Гипотеза Римана рассматривалась как один из 23 больших и сложных вопросов, стоящих перед математиками в XX столетии, и именно так ее рассматривал Давид Гильберт— вероятно, величайший среди математиков, активно работавших в 1900 году. [105] III. В главе 10.iii мы кратко упомянули причину, определявшую важность Гипотезы Римана на рубеже столетия. Основным фактором было то, что Теорема о распределении простых чисел была к этому моменту доказана. С 1896 года с математической точностью было известно, что π(N) ~ Li(N), и всеобщее внимание было приковано к этому значку «волны» посередине. Да, по мере того как N неограниченно растет, делаясь все больше и больше, π(N) пропорциональным образом становится все ближе и ближе к Li(N). Но какова природа этой близости? Нельзя ли указать лучшее приближение? И вообще, насколько приближенно это приближение? Каков «остаточный член»? Когда вопрос с ТРПЧ решился и математики смогли свободно предаваться мыслям об этих «второстепенных» вещах, они обнаружили, что их взор прикован к Гипотезе Римана. В работе Бернхарда Римана 1859 года ТРПЧ не была, конечно, доказана, но та работа явственно подсказывала, что теорема эта верна, и, более того, там предлагалось выражение для остаточного члена. В это выражение входили все нетривиальные нули дзета-функции. Точное знание о том, где, собственно, находятся эти нули, стало делом неотложной важности. Математическая суть дела будет проясняться по мере нашего продвижения вперед, но, думается, вы вовсе не удивитесь, узнав, что все эти нули — комплексные числа. В 1900 году о расположении этих нетривиальных нулей (имеется в виду расположение на комплексной плоскости) с математической точностью было известно следующее. • Существует бесконечно много нулей дзета-функции, причем все они имеют вещественную часть, заключенную в пределах от 0 до 1 (не включая границы). Чтобы наглядно это представить, математики используют комплексную плоскость (рис. 12.1) и говорят, что все нетривиальные нули лежат в критической полосе. В Гипотезе Римана делается более сильное утверждение: что все они лежат на линии, вещественная часть которой равна одной второй — т.е. на критической прямой. «Критическая полоса» и «критическая прямая» — распространенные термины при обсуждении Гипотезы Римана, и мы отныне будем свободно ими пользоваться. 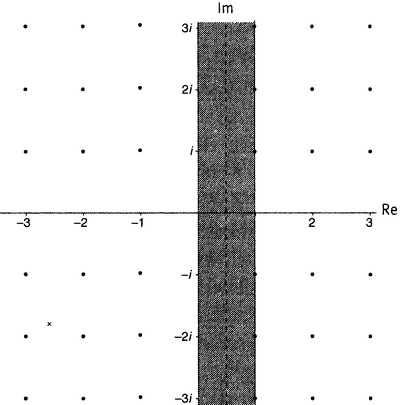
Рисунок 12.1. Критическая полоса (затемнена) и критическая прямая (показана штрихами).
|
 Вернуться к просмотру книги
Вернуться к просмотру книги
 Перейти к Оглавлению
Перейти к Оглавлению
 Перейти к Примечанию
Перейти к Примечанию
 © 2020 LoveRead.ec - электронная библиотека в которой можно
© 2020 LoveRead.ec - электронная библиотека в которой можно