
|
||
|
|
||
|
|
Онлайн книга - Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике | Автор книги - Джон Дербишир
Cтраница 47

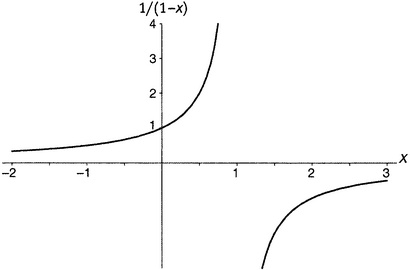
Рисунок 9.2. Функция 1/(1 − x). Но они не одно и то же, поскольку у них различные области определения, как это видно из рисунков 9.1 и 9.2. S(x) имеет значения только между −1 и 1, не включая границы; функция же 1/(1 − x) имеет значения везде, за исключением точки x = 1. Если x = 2, то ее значение равно 1/(1 − 2), то есть −1. Если x = 10, то значение равно 1/(1 − 10), то есть −1/9. Если x = −2, то значение равно 1/(1 − (−2)), то есть 1/3. Можно нарисовать график функции 1/(1 − x). Как видно, он совпадает с предыдущим графиком в промежутке между −1 и 1, но имеет еще и значения к западу от −1 (включая саму −1) и к востоку от 1. Мораль здесь в том, что бесконечный ряд может определять только часть функции; или, используя подобающие математические термины, бесконечный ряд может определять функцию только на части ее области определения. Остальная часть функции может где-то прятаться, ожидая, пока ее не вытащат на свет с помощью фокуса типа того, что мы применили к S(x). IV. Это приводит к очевидному вопросу: а не обстоит ли дело подобным же образом и с дзета-функцией? Не случилось ли так, что бесконечная сумма, которую мы использовали для дзета-функции, — выражение (9.1) — описывает только часть этой функции? И у этой функции есть что-то еще, что нам только предстоит открыть? Может ли область определения дзета-функции 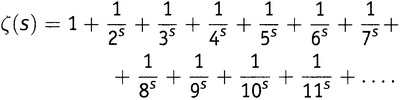
оказаться больше, чем просто «все числа, большие 1»? Конечно может. Иначе зачем бы мы тут стали влезать во все эти подробности? Да, дзета-функция имеет значения при аргументах, меньших 1. На самом деле, как и функция 1/(1 − x), она имеет значения при всех числах за единственным исключением x = 1. Сейчас подходящий момент, чтобы привести график дзета-функции, который продемонстрировал бы все ее свойства в широком интервале значений. К сожалению, это невозможно. Как уже упоминалось, кроме как для простейших функций, обычно нет хорошего и надежного способа показать функцию во всем ее великолепии. Близкое знакомство с функцией требует времени, терпения и тщательного изучения. Можно, однако, изобразить дзета-функцию по кускам. На рисунках с 9.3 по 9.10 показаны значения ζ(s) для некоторых аргументов, находящихся слева от s = 1, хотя для этого потребовалось выбрать свой собственный масштаб на каждом графике. Понять, где мы находимся, можно, руководствуясь подписанными аргументами (на горизонтальной оси) и значениями (на вертикальной оси). При обозначении масштаба m указывает на миллион, tr на триллион, mtr обозначает миллион триллионов, a btr — миллиард триллионов. Коротко говоря, когда s лишь немного меньше единицы (рисунок 9.3), значения функции очень большие по величине и отрицательные — как если бы при движении на запад при пересечении линии s = 1 значения внезапно переметнулись из бесконечности в минус бесконечность. Если продолжить путешествие по рисунку 9.3 — т.е. устремлять s ближе и ближе к нулю, — то подъем вверх радикально замедляется. Когда s равно нулю, ζ(s) равна −1/2. При s = −2 кривая пересекает ось s, т.е. ζ(s) равна нулю. 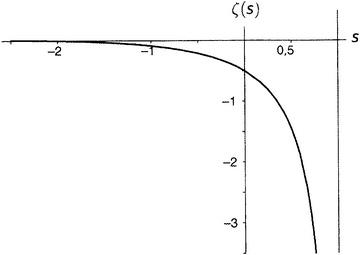
Рисунок 9.3. Затем (мы по-прежнему двигаемся на запад, добравшись теперь до рисунка 9.4) график взбирается на относительно скромную высоту (в действительности до 0,009159890…), а после этого поворачивает вниз и снова пересекает ось при s = −4. График попадает в неглубокую впадину (−0,003986441…), а после нее снова взбирается вверх и пересекает ось при s = −6. Еще один невысокий пик (0,004194…), спуск до пересечения с осью при s = −8 и далее в несколько более глубокую впадину (−0,007850880…), затем пересечение с осью в точке −10, после чего уже довольно заметный пик (0,022730748…), пересечение с осью при s = −12, впадина поглубже (−0,093717308…), пересечение с осью при s = −14 и т.д. 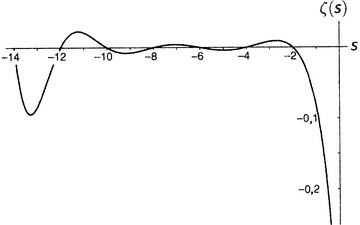
Рисунок 9.4. Дзета-функция равна нулю при каждом отрицательном четном числе, а по мере продвижения на восток (рисунки от 9.5 до 9.10) последовательные пики и впадины быстро делаются все более и более значительными. Последняя показанная впадина расположена при s = −49.587622654…, а глубина ее составляет около 305 507 128 402 512 980 000 000. Сами видите, как нелегко изобразить дзета-функцию на одном графике. 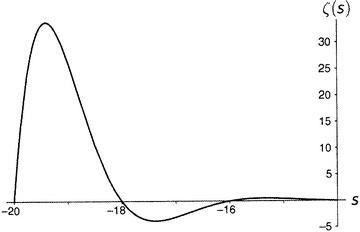
Рисунок 9.5. 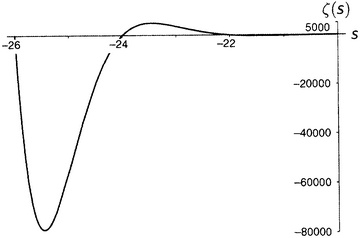
Рисунок 9.6. 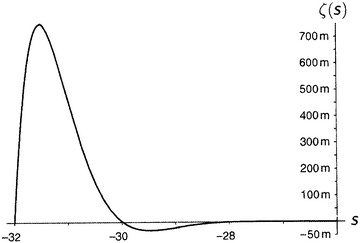
Рисунок 9.7. 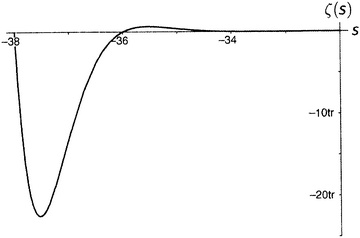
Рисунок 9.8. 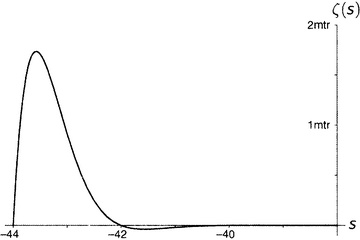
Рисунок 9.9.
|
 Вернуться к просмотру книги
Вернуться к просмотру книги
 Перейти к Оглавлению
Перейти к Оглавлению
 Перейти к Примечанию
Перейти к Примечанию
 © 2020 LoveRead.ec - электронная библиотека в которой можно
© 2020 LoveRead.ec - электронная библиотека в которой можно